题目内容
12．将函数y=cos2x的图象上所有的点向右平移$\frac{1}{2}$个单位，得到的图象所对应的函数解析式为（ ）| A． | $y=cos（2x-\frac{1}{2}）$ | B． | $y=cos（2x+\frac{1}{2}）$ | C． | y=cos（2x-1） | D． | y=cos（2x+1） |
分析 将函数y=cos2x的图象向右平移$\frac{1}{2}$个单位，得到的新函数的解析式要在x上减去平移的大小，再用诱导公式得到结果．
解答 解：∵将函数y=cos2x的图象向右平移$\frac{1}{2}$个单位，
∴解析式为y=cos2（x-$\frac{1}{2}$）=cos（2x-1）．
故选：C．
点评 本题考查三角函数图象的平移和诱导公式的应用，本题解题的关键是抓住平移的方向和大小，注意这种情况下只在自变量的系数是1的情况下加或减，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．若幂函数$f（x）=（{m^2}-3m+3）{x^{{m^2}+m-2}}$的图象不经过原点，则实数m的值为（ ）
| A． | 1或2 | B． | 1或-2 | C． | 1 | D． | 2 |
7．已知集合U={1，2，3，4，5，6}，A={2，3，5}，B={1，3，6}，则∁U（A∪B）=（ ）
| A． | {4} | B． | ϕ | C． | {1，2，4，5，6} | D． | {1，2，3，5，6} |
4．已知集合A={x|y=lg（x-1）}，B={x|x2-4≤0}，则A∩B=（ ）
| A． | {x|1＜x＜2} | B． | {x|1≤x≤3} | C． | {x|1＜x≤2} | D． | {x|1≤x≤2} |
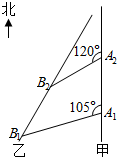如图所示，甲船以每小时30$\sqrt{2}$海里的速度向正北方向航行，乙船按固定方向匀速直线航行．当甲船位于A1处时，乙船位于甲船的南偏西75°方向的B1处，此时两船相距20海里．当甲船航行20分钟到达A2处时，乙船航行到甲船的南偏西60°方向的B2处，此时两船相距10$\sqrt{2}$海里．问：乙船每小时航行多少海里？