题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}x+4,-8≤x≤0\\{x^2}-2x,0<x≤4\\-x+2,\;4<x<6\end{array}$.(1)画出y=f(x)的图象并写出最值;
(2)求f(x)>-2的解集.
分析 (1)由分段函数的画法,作出函数f(x)的图象,通过图象可得最值;
(2)讨论-8≤x≤0,0<x≤4,4<x<6,解不等式,求并集,注意结合图象,即可得到所求解集.
解答 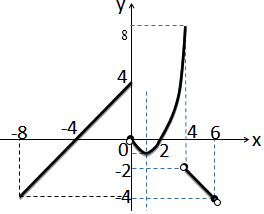 解:(1)函数f(x)=$\left\{\begin{array}{l}x+4,-8≤x≤0\\{x^2}-2x,0<x≤4\\-x+2,\;4<x<6\end{array}$,
解:(1)函数f(x)=$\left\{\begin{array}{l}x+4,-8≤x≤0\\{x^2}-2x,0<x≤4\\-x+2,\;4<x<6\end{array}$,
由分段函数的图象画法,可得函数y=f(x)的图象为:
由图象可得f(x)的最小值为-4,最大值为8;
(2)由-8≤x≤0时,x+4>-2,
可得-6<x≤0;
当0<x≤4时,x2-2x>-2恒成立,即为0<x≤4;
由4<x<6可得2-x>-2即x<4,可得x∈∅.
则解集为(-6,4].
点评 本题考查分段函数的图象和性质,主要是最值的求法,考查不等式的解法,注意结合图象,考查作图和用图能力,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
14.定义2×2矩阵$[\begin{array}{l}{a_1}\\{a_3}\end{array}\right.\left.\begin{array}{l}{a_2}\\{a_4}\end{array}]={a_1}{a_4}-{a_2}{a_3}$,若$f(x)=[{\begin{array}{l}{cosx-sinx}&{\sqrt{3}}\\{cos(\frac{π}{2}+2x)}&{cosx+sinx}\end{array}}]$,则f(x)( )
| A. | .图象关于(π,0)中心对称 | B. | 图象关于直线$x=\frac{π}{2}$对称 | ||
| C. | 在区间$[-\frac{π}{6},0]$上单调递增 | D. | 周期为π的奇函数 |
15.如图网格纸上的小正方形边长为1,粗线是一个三棱锥的三视图,则该三棱锥的外接球表面积为( )

| A. | 48π | B. | 36π | C. | 24π | D. | 12π |
3.函数y=$\frac{lnx}{2x}$的最大值为( )
| A. | $\frac{1}{2}$e-1 | B. | e | C. | e2 | D. | $\frac{5}{3}$ |
20.从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品至少有一件是次品”,则下列结论正确的是( )
| A. | A与B互斥 | B. | 任何两个均互斥 | C. | B与C互斥 | D. | 任何两个均对立 |
18.已知f(x)=x2-bx+a,且f(0)=3,f(2-x)=f(x),则下列关系成立的是( )
| A. | f(bx)≥f(ax) | B. | f(bx)≤f(ax) | ||
| C. | f(bx)<f(ax) | D. | f(bx)与f(ax)的大小关系不确定 |