题目内容
2.已知集合A={x|-2<x<5},集合$B=\left\{{x\left|{2<{{({\frac{1}{2}})}^x}<16}\right.}\right\}$,集合C={x|m+1≤x≤2m-1},(1)求A∩B,A∪B;
(2)若A∪C=A,求实数m的取值范围.
分析 (1)化简集合B,根据集合的基本运算即可求A∩B,A∪B;
(2)根据A∪C=A,建立条件关系即可求实数m的取值范围.
解答 解:(1)集合A={x|-2<x<5},集合$B=\left\{{x\left|{2<{{({\frac{1}{2}})}^x}<16}\right.}\right\}$={x|2<2-x<24}={x|-4<x<-1}
∴A∩B={x|-2<x<-1},
A∪B={x|-4<x<5}.
(2)集合C={x|m+1≤x≤2m-1},
∵A∪C=A,
∴C⊆A,
当C=∅时,满足题意,此时m+1>2m-1,解得:m<2.
当C≠∅时,要使C⊆A成立,需满足$\left\{\begin{array}{l}{-2≤m+1}\\{m+1≤2m-1}\\{2m-1≤5}\end{array}\right.$,
解得:2≤m≤3
综上可得实数m的取值范围是(-∞,3].
点评 本题主要考查集合的基本运算,比较基础.

练习册系列答案
相关题目
11.若a=log20.5,b=20.5,c=0.52,则a,b,c三个数的大小关系是( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
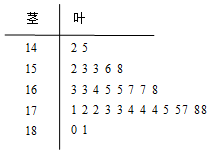 从某校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图(单位:cm):若高一年级共有600人,据上图估算身高在1.70m以上的大约有300人.
从某校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图(单位:cm):若高一年级共有600人,据上图估算身高在1.70m以上的大约有300人.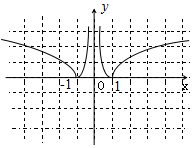 已知函数f(x)是定义在{x|x≠0}上的偶函数,且当x>0时,f(x)=log2x.
已知函数f(x)是定义在{x|x≠0}上的偶函数,且当x>0时,f(x)=log2x.