题目内容
已知平面上的线段l及点P,任取l上一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作d(P,l).
(Ⅰ)求点P(1,1)到线段l:x-y-3=0,(3≤x≤5)的距离d(P,l);
(Ⅱ)设l是长为2的线段,求点的集合D={P|d(P,l)≤1}所表示的图形面积;
(Ⅲ)写出到两条线段l1,l2距离相等的点的集合Ω={P|d(P,l1)=d(P,l2)},并在直角坐标系中作出相应的轨迹.其中l1=AB,l2=CD,A(1,3),B(1,0),C(-1,3),D(-1,-2).
(Ⅰ)求点P(1,1)到线段l:x-y-3=0,(3≤x≤5)的距离d(P,l);
(Ⅱ)设l是长为2的线段,求点的集合D={P|d(P,l)≤1}所表示的图形面积;
(Ⅲ)写出到两条线段l1,l2距离相等的点的集合Ω={P|d(P,l1)=d(P,l2)},并在直角坐标系中作出相应的轨迹.其中l1=AB,l2=CD,A(1,3),B(1,0),C(-1,3),D(-1,-2).
考点:轨迹方程
专题:综合题,直线与圆
分析:(Ⅰ)根据d(P,l)的定义,结合两点间的距离公式和二次函数的性质,即可算出的值d(P,l).
(Ⅱ)d(P,AB)≤1,即Q在线段AB上时线段PQ长度的最小值不超过1,由此结合点A、B的坐标,利用距离公式即可化简出所求图形的边界曲线方程,结合矩形面积与圆面积公式可得该图形的面积;
(Ⅲ)根据所给的四个点的坐标,写出两条直线的方程,从直线方程中看出这两条直线之间的平行关系,得到要求的结果.
(Ⅱ)d(P,AB)≤1,即Q在线段AB上时线段PQ长度的最小值不超过1,由此结合点A、B的坐标,利用距离公式即可化简出所求图形的边界曲线方程,结合矩形面积与圆面积公式可得该图形的面积;
(Ⅲ)根据所给的四个点的坐标,写出两条直线的方程,从直线方程中看出这两条直线之间的平行关系,得到要求的结果.
解答:
解:(Ⅰ)设Q(x,x-3)是线段l:x-y-3=0(3≤x≤5)上一点,则
|PQ|=
=
,(3≤x≤5)
当x=3时,d(P,l)=|PQ|最小值=
.
(Ⅲ)点集D由如下曲线围成
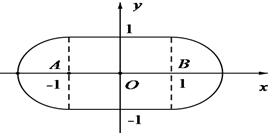
l1:y=1(|x|≤1),l2:y=-1(|x|≤1),
C1:(x+1)2+y2=1(x≤-1),C2:(x-1)2+y2=1(x≥1),
其面积为S=4+π.
(Ⅲ)利用两点式写出两条直线的方程,AB:x=1,CD:x=-1,
到两条线段l1,l2距离相等的点的集合Ω={P|d(P,l1)=d(P,l2)},
根据两条直线的方程可知两条直线之间的关系是平行,
∴得到到两条线段距离相等的点是y轴非负半轴,抛物线x=
y2(y≤0,0≤x≤1),直线y=-x-1(x>1).
如图所示

|PQ|=
| (x-1)2+(x-4)2 |
2(x-
|
当x=3时,d(P,l)=|PQ|最小值=
| 5 |
(Ⅲ)点集D由如下曲线围成

l1:y=1(|x|≤1),l2:y=-1(|x|≤1),
C1:(x+1)2+y2=1(x≤-1),C2:(x-1)2+y2=1(x≥1),
其面积为S=4+π.
(Ⅲ)利用两点式写出两条直线的方程,AB:x=1,CD:x=-1,
到两条线段l1,l2距离相等的点的集合Ω={P|d(P,l1)=d(P,l2)},
根据两条直线的方程可知两条直线之间的关系是平行,
∴得到到两条线段距离相等的点是y轴非负半轴,抛物线x=
| 1 |
| 4 |
如图所示

点评:本题给出点P到线段l的距离的定义,求实际问题中的距离并讨论相应的曲线方程.着重考查了点到直线的距离公式、二次函数的性质和曲线与方程的化简等知识,属于中档题.

练习册系列答案
相关题目
下列各个图形中,异面直线的画法不妥的是(( )
A、 |
B、 |
C、 |
D、 |
 在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、BB1的中点,求△DMN的面积.
在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是棱A1B1、BB1的中点,求△DMN的面积. 如图所示,过圆O:x2+y2=4与y轴正半轴的交点A作圆的切线l,M为l上任意一点,再过M作圆的另一切线,切点为Q,当点M在直线l上移动时,求三角形MAQ的垂心的轨迹方程.
如图所示,过圆O:x2+y2=4与y轴正半轴的交点A作圆的切线l,M为l上任意一点,再过M作圆的另一切线,切点为Q,当点M在直线l上移动时,求三角形MAQ的垂心的轨迹方程. 如图,过抛物线C1:x2=2py(p>0)上第一象限内的点P作C1的切线,依次交抛物线C2:x2=-2py于点Q,R,过Q,R分别作C2的切线,两条切线交于点M.
如图,过抛物线C1:x2=2py(p>0)上第一象限内的点P作C1的切线,依次交抛物线C2:x2=-2py于点Q,R,过Q,R分别作C2的切线,两条切线交于点M.