题目内容
16.设函数f(x)满足f(x+2π)=f(x),f(0)=0,则f(4π)=( )| A. | 0 | B. | π | C. | 2π | D. | 4π |
分析 由已知可得函数的周期为2π,进而可得f(4π)=f(2π)=f(0).
解答 解:∵函数f(x)满足f(x+2π)=f(x),
∴f(4π)=f(2π)=f(0)=0,
故选:A.
点评 本题考查的知识点是函数的周期性,函数求值,难度不大,属于基础题.

练习册系列答案
相关题目
8.若四棱锥P-ABCD的三视图如图所示,则它的体积为( )
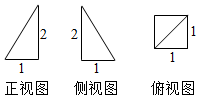

| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |