题目内容
16.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ-4cosθ=0.(1)求直线l与曲线C的普通方程;
(2)已知直线l与曲线C交于A,B两点,设M(2,0),求|$\frac{1}{|MA|}$-$\frac{1}{|MB|}$|的值.
分析 (1)利用三种方程的转化方法,求直线l与曲线C的普通方程;
(2)直线l的参数方程为$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),代入y2=4x,整理可得3t2-8t-32=0,利用参数的几何意义,求|$\frac{1}{|MA|}$-$\frac{1}{|MB|}$|的值.
解答 解:(1)直线l的参数方程为$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),消去参数,可得普通方程y=$\sqrt{3}$(x-2);
曲线C的极坐标方程为ρsin2θ-4cosθ=0,直角坐标方程为y2=4x;
(2)直线l的参数方程为$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),代入y2=4x,整理可得3t2-8t-32=0,
设A、B对应的参数分别为t1,t2,则t1+t2=$\frac{8}{3}$,t1t2=-$\frac{32}{3}$,
∴|$\frac{1}{|MA|}$-$\frac{1}{|MB|}$|=|$\frac{{t}_{1}+{t}_{2}}{{t}_{1}{t}_{2}}$|=$\frac{1}{4}$.
点评 本题考查的知识点是圆的极坐标方程,直线的参数方程,直线参数方程中参数的几何意义,难度中档.

练习册系列答案
相关题目
8.已知函数$f(x)=\left\{{\begin{array}{l}{1-|x-1|(x≤2)}\\{{e^{x-2}}(-{x^2}+8x-12)(x>2)}\end{array}}\right.$,如在区间(1,+∞)上存在n(n≥2)个不同的数x1,x2,x3,…,xn,使得比值$\frac{f({x}_{1})}{{x}_{1}}$=$\frac{f({x}_{2})}{{x}_{2}}$=…=$\frac{f({x}_{n})}{{x}_{n}}$成立,则n的取值集合是( )
| A. | {2,3,4,5} | B. | {2,3} | C. | {2,3,5} | D. | {2,3,4} |
8.设i为虚数单位,则复数z=$\frac{1+2i}{i}$的虚部为( )
| A. | -2 | B. | -i | C. | i | D. | -1 |
4.设i为虚数单位,若复数$\frac{i}{1+i}$的实部为a,复数(1+i)2的虚部为b,则复数z=a-bi在复平面内的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 (
( ),若
),若 且在
且在 上有且仅有三个零点,则
上有且仅有三个零点,则 ( )
( ) B.2 C.
B.2 C. D.
D.
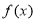 是定义在
是定义在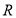 上的偶函数,且在区间
上的偶函数,且在区间 上单调递增,若实数
上单调递增,若实数 满足
满足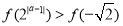 ,则
,则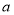 的取值范围是( )
的取值范围是( )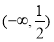 B.
B.
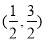 D.
D.
 的图象大致是( )
的图象大致是( ) B.
B. C.
C. D.
D.
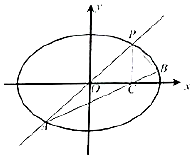 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.