题目内容
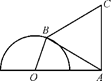
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.问:点B在什么位置时,四边形OACB面积最大?

点B在使∠AOB=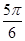 的位置时,四边形OACB面积最大
的位置时,四边形OACB面积最大
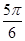 的位置时,四边形OACB面积最大
的位置时,四边形OACB面积最大试题分析:在
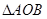 中,由已知OA=2,OB=1,设∠AOB=
中,由已知OA=2,OB=1,设∠AOB=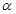 ,则可应用余弦定理将AB的长用
,则可应用余弦定理将AB的长用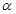 的三角函数表示出来,进而四边形OACB面积S=S△AOB+S△AB表示成为
的三角函数表示出来,进而四边形OACB面积S=S△AOB+S△AB表示成为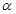 的三角函数,再注意
的三角函数,再注意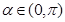 将三角函数化简成为
将三角函数化简成为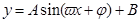 的形式,就可求得使四边形OACB面积最大的角
的形式,就可求得使四边形OACB面积最大的角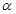 的值,从而就可确定点B的位置.
的值,从而就可确定点B的位置.试题解析:设∠AOB=α, .1分
在△AOB中,由余弦定理得
AB2=OA2+OB2-2×OA×OBcos∠AOB
=12+22-2×1×2×cosα
=5-4cosα, .4分
于是,四边形OACB的面积为
S=S△AOB+S△ABC=
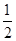 OA·OBsinα+
OA·OBsinα+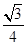 AB2 6分
AB2 6分=
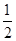 ×2×1×sinα+
×2×1×sinα+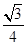 (5-4cosα)
(5-4cosα)=sinα-
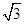 cosα+
cosα+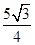
=2sin
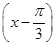 +
+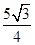 . .10分
. .10分因为0<α<π,所以当α-
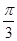 =
=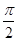 ,α=
,α=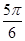 ,
,即∠AOB=
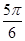 时,四边形OACB面积最大12分 12分
时,四边形OACB面积最大12分 12分
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,并写出函数
,并写出函数 的最小正周期;
的最小正周期;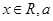 为非零常数,且
为非零常数,且 ,试问
,试问 是周期函数吗?证明你的结论.
是周期函数吗?证明你的结论. 其中
其中
 在
在 中,
中, 分别是角的对边,且
分别是角的对边,且 .
. ,
, ,求
,求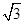 sinA)cosB=0.
sinA)cosB=0. ,BD=
,BD= ,周长为18,则这个平行四边形的面积为( )
,周长为18,则这个平行四边形的面积为( )
 斜边AB上的三等分点,则tan
斜边AB上的三等分点,则tan ECF=( )
ECF=( )

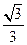

 .
.