题目内容
已知函数f(x)=ax2-2x+1在[-1,2]上的最大值为3,求a的值.
考点:二次函数的性质
专题:函数的性质及应用
分析:由函数f(x)的最大值为3,分别讨论(1)若f(-1)=3,(2)若f(2)=3,(3)若f(
)=3的情况,从而求出a的值.
| 1 |
| a |
解答:
解:∵函数f(x)=ax2-2x+1在[-1,2]上的最大值为3,
∴(1)若f(-1)=3则a+2+1=3,a=0,
而a=0时,函数f(x)=-2x+1 在[-1,2]的最大值为3
(2)若f(2)=3,则4a-4+1=3 a=
而a=
时,函数f(x)=
x2-2x+1=
(x-
)2+
在[-1,2]的最大值为
(3)若f(
)=3则
-
+1=3a=-
而a=-
时,函数f(x)=-
x2-2x+1=-
(x+2)2+3在[-1,2]的最大值为
综上可知a=0.
∴(1)若f(-1)=3则a+2+1=3,a=0,
而a=0时,函数f(x)=-2x+1 在[-1,2]的最大值为3
(2)若f(2)=3,则4a-4+1=3 a=
| 3 |
| 2 |
而a=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 9 |
| 2 |
(3)若f(
| 1 |
| a |
| 1 |
| a |
| 2 |
| a |
| 1 |
| 2 |
而a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
综上可知a=0.
点评:本题考查了二次函数的性质,考查了函数的最值问题,是一道基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
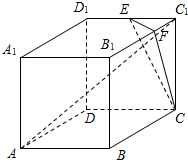 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,∠DAB=45°,AA1=AB=2,AD=2
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,∠DAB=45°,AA1=AB=2,AD=2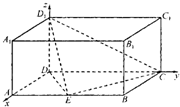 (文科)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz.
(文科)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=2,AB=4,E为AB的中点.分别以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz.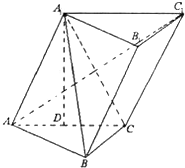 如图,斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,BA1⊥AC1,点A1在底面ABC上的射影恰为AC的中点D.
如图,斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,BA1⊥AC1,点A1在底面ABC上的射影恰为AC的中点D. 图中的三个直角三角形是一个几何体的三视图,
图中的三个直角三角形是一个几何体的三视图,