题目内容
17.在△ABC中,AB=5,AC=6,BC=7,S△ABC=6$\sqrt{6}$,O是△ABC的内心,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中0≤x≤1,0≤y≤1,则动点P的轨迹所覆盖的面积是( )| A. | $\frac{{10\sqrt{6}}}{3}$ | B. | $\frac{{5\sqrt{6}}}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{20}{3}$ |
分析 由题意可知动点P的轨迹为以OA,OB为邻边的平行四边形ADBO的内部(含边界).根据三角形的面积公式即可求得△ABC内切圆半径为r,求得△AOB的面积,
解答  解:$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中0≤x≤1,0≤y≤1,
解:$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中0≤x≤1,0≤y≤1,
∴动点P的轨迹为以OA,OB为邻边的平行四边形ADBO的内部(含边界).
AB=5,AC=6,BC=7,S△ABC=6$\sqrt{6}$,
设△ABC内切圆半径为r,则$\frac{1}{2}$(5+6+7)r=6$\sqrt{6}$,
∴r=$\frac{2\sqrt{6}}{3}$,
∴S△AOB=$\frac{1}{2}$×AB×r=$\frac{1}{2}$×5×$\frac{2\sqrt{6}}{3}$=$\frac{5\sqrt{6}}{3}$,
∴动点P的轨迹所覆盖的面积为:2S△AOB=$\frac{10\sqrt{6}}{3}$,
故选A.
点评 本题考查三角形的面积公式,向量在几何中的应用,考查计算能力,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
7.下列命题:
①“x=2”是“x2-4x+4=0”的必要不充分条件;
②“圆心到直线的距离等于半径”是“这条直线为圆的切线”的充分必要条件;
③“sin α=sin β”是“α=β”的充要条件;
④“ab≠0”是“a≠0”的充分不必要条件.
其中为真命题的是( )
①“x=2”是“x2-4x+4=0”的必要不充分条件;
②“圆心到直线的距离等于半径”是“这条直线为圆的切线”的充分必要条件;
③“sin α=sin β”是“α=β”的充要条件;
④“ab≠0”是“a≠0”的充分不必要条件.
其中为真命题的是( )
| A. | ①③ | B. | ②④ | C. | ②③ | D. | ①③ |
5.已知x∈[0,π],f(x)=sin(cosx)的最大值为a,最小值为b,g(x)=cos(sinx)的最大 值为c,最小值为d,则( )
| A. | b<d<a<c | B. | d<b<c<a | C. | b<d<c<a | D. | d<b<a<c |
9.若函数f(x)=$\left\{\begin{array}{l}(2b-1)•{3^x}-b,x>0\\-{x^2}+(2-b)x,x≤0\end{array}$在R上为增函数,则实数b的取值范围为( )
| A. | $(\frac{1}{2},2]$ | B. | [1,2] | C. | (1,2] | D. | $(\frac{1}{2},2)$ |
6.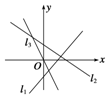 如图直线l1,l2,l3的倾斜角分别为α1,α2,α3,则有( )
如图直线l1,l2,l3的倾斜角分别为α1,α2,α3,则有( )
 如图直线l1,l2,l3的倾斜角分别为α1,α2,α3,则有( )
如图直线l1,l2,l3的倾斜角分别为α1,α2,α3,则有( )| A. | α1<α2<α3 | B. | α1<α3<α2 | C. | α3<α2<α1 | D. | α2<α1<α3 |