题目内容
16.从含有两件正品a,b和一件次品c的3件产品中每次任取一件,连续取两次,求取出的两件产品中恰有一件是次品的概率.(1)每次取出不放回;
(2)每次取出后放回.
分析 (1)每次取出一个,取后不放回地连续取两次,其一切可能的结果组成的基本事件有6个,可以列举出所有的事件,从列举出的事件中看出取出的两件中,恰好有一件次品的事件数,得到概率.
(2)根据题意用列举法解题,记两件产品中恰有一件是次品为事件A,依次列举所有的基本事件,可得其情况数目,分析可得事件A的情况数目,由等可能事件的概率公式,计算可得答案.
解答 解 (1)每次取出不放回的所有结果有:
(a,b),(a,c),(b,a),(b,c),(c,a),(c,b),
其中左边的字母表示第一次取出的产品,
右边的字母表示第二次取出的产品,共有6个基本事件,
其中恰有一件次品的事件有4个,所以每次取出不放回,
取出的两件产品中恰有一件是次品的概率为$\frac{4}{6}$=$\frac{2}{3}$.
(2)每次取出后放回的所有结果:
(a,a),(a,b),(a,c),(b,a),(b,b),
(b,c),(c,a),(c,b),(c,c)共有9个基本事件,
其中恰有一件次品的事件有4个,所以每次取出后放回,
取出的两件产品中恰有一件是次品的概率为$\frac{4}{9}$.
点评 本题考查等可能事件的概率,涉及列举法的运用;注意本题是有放回抽样,共9种情况.

练习册系列答案
相关题目
7.已知集合A={x|x2-3x<0},B={-1,0,1,2,3},则A∩B=( )
| A. | {-1} | B. | {1,2} | C. | {0,3} | D. | {-1,1,2,3} |
4.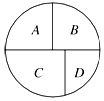 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.| A. | 120种 | B. | 150 种 | C. | 180 种 | D. | 240 种 |
11.下列函数中,在(0,+∞)内为增函数的是( )
| A. | y=sin x | B. | y=xe2 | C. | y=x3-x | D. | y=ln x-x |
1.若经过点A(3,a)、B(4,-4)的直线与经过点C(-2,0)且斜率为2的直线垂直,则a的值为( )
| A. | -$\frac{7}{2}$ | B. | $\frac{15}{4}$ | C. | 10 | D. | -10 |
1.直线ax+y-5=0截圆C:x2+y2-4x-2y+1=0的弦长为4,则a=( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |