题目内容
9.在正四面体的4个面上分别写着1,2,3,4.将4个这样的均匀正四面体投掷于桌面上,与桌面接触的4个面上的4个数的乘积被4整除的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{9}{64}$ | C. | $\frac{1}{16}$ | D. | $\frac{13}{16}$ |
分析 在正四面体的4个面上分别写着1,2,3,4.将4个这样的均匀正四面体投掷于桌面上,基本事件总数n=4×4×4×4=256,桌面接触的4个面上的4个数的乘积不能被4整除的情况有两类:没有2和4或只有一个2且没有4,没有2和4的情况有24=16种,只有一个2且没有4的情况有${C}_{4}^{1}•{2}^{3}$=32种情况,由此利用对立事件概率计算公式能求出与桌面接触的4个面上的4个数的乘积被4整除的概率.
解答 解:在正四面体的4个面上分别写着1,2,3,4.
将4个这样的均匀正四面体投掷于桌面上,
基本事件总数n=4×4×4×4=256,
桌面接触的4个面上的4个数的乘积不能被4整除的情况有两类:
没有2和4或只有一个2且没有4,
没有2和4的情况有24=16种,
只有一个2且没有4的情况有${C}_{4}^{1}•{2}^{3}$=32种情况,
所以与桌面接触的4个面上的4个数的乘积被4整除的概率:
P=1-$\frac{16+32}{256}$=$\frac{13}{16}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
4.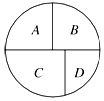 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.| A. | 120种 | B. | 150 种 | C. | 180 种 | D. | 240 种 |
4.下列各组向量互相垂直的是( )
| A. | $\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-2,-4,1) | B. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(0,0,0) | ||
| C. | $\overrightarrow{a}$=(1,2,$\frac{1}{2}$),$\overrightarrow{b}$=($\frac{1}{2}$,-$\frac{1}{2}$,1) | D. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(-2,-4,-5) |
1.直线ax+y-5=0截圆C:x2+y2-4x-2y+1=0的弦长为4,则a=( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
18.函数f(x)=x2+bx-3(b∈R)的零点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
19.如图是某一几何体的三视图,则这个几何体的侧面积和体积分别是( )


| A. | 8$\sqrt{2}$+2$\sqrt{5}$+6,8 | B. | 2$\sqrt{2}$+8$\sqrt{5}$+6,8 | C. | 4$\sqrt{2}$+8$\sqrt{5}$+12,16 | D. | 8$\sqrt{2}$+4$\sqrt{5}$+12,16 |