题目内容

12．某几何体的正视图和侧（左）视图都是边长为2的正方体，俯视图是扇形，体积为2π，该几何体的表面积为（　　）
A．8+4πB．4+4πC．8+2πD．4+2π

分析 根据三视图的特点可知几何体为圆柱的一部分，高为2，根据体积得出底面积为π，由正视图与侧视图均为正方形可得底面扇形圆心角为90°，半径为2．

解答 解：由三视图可知几何体为高h=2的圆柱的一部分，设底面积为S底．则2S=2π，∴S底=π．
∵几何体的主视图与侧视图都是边长为2的正方形，S底=π
∴底面扇形的圆心角为90°，半径r=2．
∴几何体的表面积S=2S底+2rh+$\frac{1}{4}×2πrh$=2π+8+2π=8+4π．
故选A．

点评 本题考查了空间图形的三视图，根据底面积和三视图特点求出底面半径和圆心角是解题关键．

练习册系列答案
相关题目
2．存在函数f（x）满足对任意的x∈R都有（　　）
A．f（|x|）=x+1B．f（x2+4x）=|x+2|C．f（2x2+1）=xD．f（cosx）=$\sqrt{x}$
3．直线l过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点F，且与此椭圆交于点A，B，若椭圆上存在一点M，使得$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OM}$（O为坐标原点）．
（1）求椭圆的离心率的取值范围；
（2）椭圆上是否存在这样一点M，使得四边形OAMB为矩形，如果存在，试求出M的坐标；如果不存在，请说明理由．
20．已知数列{an}满足a1=1，且9an+1an-2•an+1-4an+1=0 （n∈N*）．
（1）求a2，a3，a4的值；
（2）求{an}的通项公式．
7．已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦距是实轴长的2倍．若抛物线C2：x2=2py（p＞0）的焦点到双曲线C1的渐近线的距离为2，则抛物线C2的方程为x2=16y．
17．已知向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（0，1），若（k$\overrightarrow{a}+\overrightarrow{b}$）⊥（3$\overrightarrow{a}-\overrightarrow{b}$），则实数k=（　　）
A．-3B．3C．-$\frac{1}{3}$D．$\frac{1}{3}$
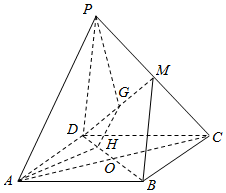4．如图，P是菱形ABCD所在平面外一点，∠BAD=60°，△PCD是等边三角形，AB=2，PA=2$\sqrt{2}$，M是PC的中点，点G为线段DM上一点（端点除外），平面APG与BD交于点H．
（Ⅰ）求证：PA∥GH；
（Ⅱ）求证：平面PAC⊥平面BDM；
（Ⅲ）求几何体M-BDC的体积．
1．已知正项数列{an}，a1=2，（an+1）an+2=1，a2=a6，则a11+a12=$\frac{1}{9}$+$\frac{\sqrt{5}}{2}$．
1．在△ABC中，a，b，c分别为角A，B，C的对边，cos2A=cosA．
（Ⅰ）求角A；
（Ⅱ）当a=2$\sqrt{3}$，S△ABC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{4\sqrt{3}}$时，求边c的值和△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网