题目内容
(本小题满分12分)在四棱锥 ,
, 平面ABCD,PA=2.
平面ABCD,PA=2.

(I)设平面 平面
平面 ,求证:
,求证: ;
;
(II)设点Q为线段PB上一点,且直线QC与平面PAC所成角的正切值为 ,求
,求 的值.
的值.
(Ⅰ)证明略;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)利用线面平行的判定定理与性质进行证明;(Ⅱ)建立空间直角坐标系,利用空间向量进行求解.
试题解析:(Ⅰ)证明:∵ 平面
平面 平面
平面 ,
,

因为 平面PCD,平面PAB
平面PCD,平面PAB 平面PCD=m
平面PCD=m
 4分
4分
(Ⅱ)设 因为
因为 ,所以建立如图所示的空间直角坐标系
,所以建立如图所示的空间直角坐标系

设 Q(x,y,z),直线QC与平面PAC所成角为θ.
所以 ,
,
所以即Q(2 ,0,-2
,0,-2 +2) 6分
+2) 6分
所以
 7分
7分
平面 的一个法向量为
的一个法向量为 . 9分
. 9分
 ,
,
解得 ∈
∈ 11分
11分
所以 =
=  .
.
考点:1.线面平行的判定与性质;2.空间向量在立体几何中的应用.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 和圆
和圆 的位置关系为
的位置关系为 ,
, ,则
,则
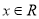 ,
,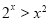 ;
; 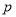 且
且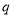 ”为假命题,则
”为假命题,则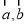 的夹角是钝角”的充分不必要条件是“
的夹角是钝角”的充分不必要条件是“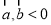 ”;
”;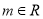 ,使
,使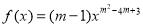 是幂函数,且在
是幂函数,且在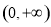 上是递减的.
上是递减的. 对应的点位于 ( )
对应的点位于 ( ) 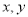 满足约束条件
满足约束条件 ,若目标函数
,若目标函数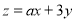 仅在点(1,0)处取得最小值,则a的取值范围为_________.
仅在点(1,0)处取得最小值,则a的取值范围为_________.
 B.
B.  C.
C.  D.
D. 
 }的前
}的前 项和为
项和为 ,若
,若 ,则公比
,则公比 =_______
=_______ :
: ,
, 的一边
的一边 为圆
为圆 长度的最大值是 .
长度的最大值是 .