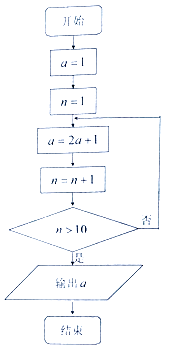
题目内容
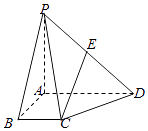
【题目】已知正三角形ABC的边长为2,AM是边BC上的高,沿AM将△ABM折起,使得二面角B﹣AM﹣C的大小为90°,此时点M到平面ABC的距离为 .
【答案】![]()
【解析】解:∵正三角形ABC的边长为2,AM是边BC上的高,
沿AM将△ABM折起,使得二面角B﹣AM﹣C的大小为90°,
∴MA、MB、MC三条直线两两垂直,AM= ![]() ,BM=CM=1,
,BM=CM=1,
以M为原点,MB,MC,MA为x轴,y轴,z轴,建立空间直角坐标系,
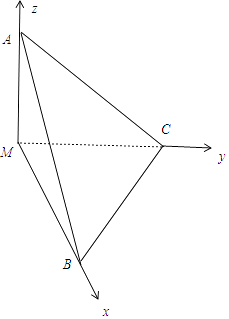
则M(0,0,0),B(1,0,0),C(0,1,0),
A(0,0, ![]() ),
),
![]() =(﹣1,0,0),
=(﹣1,0,0), ![]() =(﹣1,0,
=(﹣1,0, ![]() ),
), ![]() =(﹣1,1,0),
=(﹣1,1,0),
设平面ABC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 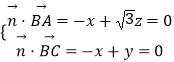 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ,
, ![]() ,1),
,1),
∴点M到平面ABC的距离为:
d= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B,A>0,ω>0,|φ|< ![]() 在某一个周期的图象时,列表并填入了部分数据,如表:
在某一个周期的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin(ωx+φ)+B | 0 |
| 0 | ﹣ | 0 |
(1)请求出上表中的x1 , x2 , x3 , 并直接写出函数f(x)的解析式;
(2)若3sin2 ![]() ﹣
﹣ ![]() mf(
mf( ![]() ﹣
﹣ ![]() )≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.
)≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.