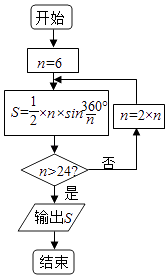
题目内容
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(cosα,sinα),设
=(cosα,sinα),设 ![]() =
= ![]() +t
+t ![]() (t为实数).
(t为实数).
(1)若 ![]() ,求当|
,求当| ![]() |取最小值时实数t的值;
|取最小值时实数t的值;
(2)若 ![]() ⊥
⊥ ![]() ,问:是否存在实数t,使得向量
,问:是否存在实数t,使得向量 ![]() ﹣
﹣ ![]() 和向量
和向量 ![]() 的夹角为
的夹角为 ![]() ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由.
【答案】
(1)解:因为a= ![]() ,所以
,所以 ![]() =(
=( ![]() ),
), ![]()
![]() =
= ![]() ,
,
则 ![]() =
= ![]() =
= ![]() =
= ![]() =
= 
所以当 ![]() 时,
时, ![]() 取到最小值,最小值为
取到最小值,最小值为 ![]() .
.
(2)解:由条件得cos45°= 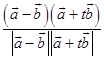 ,
,
又因为 ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
( ![]() )(
)( ![]() )=5﹣t,则有
)=5﹣t,则有 ![]() =
= ![]() ,且t<5,
,且t<5,
整理得t2+5t﹣5=0,所以存在t= ![]() 满足条件.
满足条件.
【解析】(1)先把a= ![]() 代入求出向量
代入求出向量 ![]() 的坐标,再把
的坐标,再把 ![]() 转化为
转化为 ![]() =
= ![]() ,把所求结论以及已知条件代入得到关于实数t的二次函数,利用配方法求出
,把所求结论以及已知条件代入得到关于实数t的二次函数,利用配方法求出 ![]() 的最小值以及实数t的值;(2)先利用向量垂直求出
的最小值以及实数t的值;(2)先利用向量垂直求出 ![]() 以及
以及 ![]() 和(
和( ![]() )(
)( ![]() ),代入cos45°=
),代入cos45°= 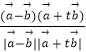 ,可得关于实数t的方程,解方程即可求出实数t.
,可得关于实数t的方程,解方程即可求出实数t.
【考点精析】掌握数量积表示两个向量的夹角是解答本题的根本,需要知道设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则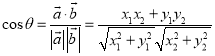 .
.

【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 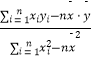 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.