题目内容
已知△ABC，向量
=(2-k，3)，
=(2，4)，且|
|≤4，k∈Z，求△ABC为直角三角形的概率．
| BC |
| AC |
| AB |
分析：本题考查的知识点是古典概型，我们根据 |
|≤4及k∈Z易求出满足条件的所有的k，然后分类讨论△ABC是直角三角形时k的取值情况，然后代入古典概型计算公式，即可得到答案．
| AB |
解答：（本小题满分12分）
解：∵
=(2-k，3)∴
=(k-2，-3)，∴
=
+
=(k，1)．…（2分）
又∵|
|≤4，∴k2+1≤16，k2≤15，∴-
≤k≤
．…（4分）
又∵k∈Z，∴k=0，±1，±2，±3．…（5分）
若△ABC为直角三角形，则
（i）
•
=0，∴2k+4=0，∴k=-2；…（6分）
（ii）
•
=0，∴k2-2k-3，∴k=3或-1；…（8分）
（iii）
•
=0，∴2（2-k）+12=0，∴k=8（舍去）…（9分）
∴△ABC为直角三角形的k的值为-1，-2，3，而基本事件总数为7…（10分）
由古典概型知，P=
．
即△ABC为直角三角形的概率为
．…（12分）
解：∵
| BC |
| CB |
| AB |
| AC |
| CB |
又∵|
| AB |
| 15 |
| 15 |
又∵k∈Z，∴k=0，±1，±2，±3．…（5分）
若△ABC为直角三角形，则
（i）
| AB |
| AC |
（ii）
| AB |
| BC |
（iii）
| AC |
| BC |
∴△ABC为直角三角形的k的值为-1，-2，3，而基本事件总数为7…（10分）
由古典概型知，P=
| 3 |
| 7 |
即△ABC为直角三角形的概率为
| 3 |
| 7 |
点评：解决问题的步骤是：计算满足条件的基本事件个数，及基本事件的总个数，然后代入古典概型计算公式进行求解，同时考查了分类讨论的数学思想，属于中档题．
练习册系列答案
相关题目
与
满足(
)·
=0,且
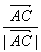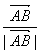,则△ABC为