题目内容
7. 如图,在四面体ABCD中,△ABD,△ACD,△DBC和△ABC全等,且AB=AC=$\sqrt{3}$,BC=2;求证:平面BCD⊥平面ABC.
如图,在四面体ABCD中,△ABD,△ACD,△DBC和△ABC全等,且AB=AC=$\sqrt{3}$,BC=2;求证:平面BCD⊥平面ABC.
分析 欲证明平面BCD⊥平面ABC,首先根据二面角的平面角的定义构造出对应的二面角A-BC-D的平面角,求出二面角A-BC-D的大小为90°,从而得到平面BCD⊥平面ABC.
解答 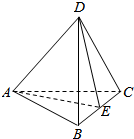 证明:取BC的中点E,连结AE、DE.∵AB=AC,∴AE⊥BC.
证明:取BC的中点E,连结AE、DE.∵AB=AC,∴AE⊥BC.
又△ABD≌△DBC,AB=AC,
∴DB=DC,DE⊥BC.
∴∠AED为二面角ABCD的平面角.
又△ABC≌△DBC,且△ABC是以BC为底的等腰三角形,
△DBC也是以BC为底的等腰三角形,所以AB=AC=DB=DC=$\sqrt{3}$.
又△ABD≌△BDC,∴AD=BC=2.
在Rt△DEB中,DB=$\sqrt{3}$,BE=1,
∴DE=$\sqrt{D{B}^{2}-B{E}^{2}}$=$\sqrt{2}$,
同理,AE=$\sqrt{2}$.
在△AED中,AE=DE=$\sqrt{2}$,AD=2,
∴AD2+DE2=AD2,∠AED=90°,
∴二面角A-BC-D的大小为90°.
∴平面BCD⊥平面ABC.
点评 本题考查面面垂直的证明,考虑根据二面角的平面角的定义构造出相应的平面角,而在构造过程中,往往离不开添加垂线,利用线面垂直、面面垂直关系从而达到目的,最后问题通常转化为解三角形.

练习册系列答案
相关题目
17.已知函数f(x)=x3+bx2+cx+d的图象如图所示,则函数y=log${\;}_{\frac{1}{2}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调减区间为( )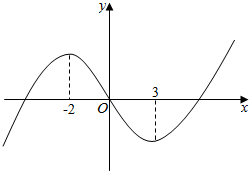

| A. | ($\frac{1}{2}$,+∞) | B. | (3,+∞) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-2) |
 如图所示,有一个堤坝,原斜坡AB长50m,坡角∠ABC=40°,现要将斜坡的坡角改成25°,即∠D=25°,那么斜坡的坡底要延长多少(精确到0.1m)?
如图所示,有一个堤坝,原斜坡AB长50m,坡角∠ABC=40°,现要将斜坡的坡角改成25°,即∠D=25°,那么斜坡的坡底要延长多少(精确到0.1m)?