题目内容
正三棱锥侧棱与底面所成角的大小为45°,若该三棱锥的体积为
,则它的表面积为 .
| 2 |
| 3 |
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:计算题,空间位置关系与距离
分析:由题意,顶点在底面中的射影是底面的中心,从而利用侧棱与底面所成角为45°角,设底面边长为3a,可求高,从而得解
解答:
解:设底面边长为3a,则
由题意,顶点在底面中的射影是底面的中心,从而有高为
a,
∵三棱锥的体积为
,
∴
•
•9a2•
a=
,
∴a3=
,
∵斜高为
a,
∴表面积为
a2+
×9a×
a=
.
故答案为:
.
由题意,顶点在底面中的射影是底面的中心,从而有高为
| 3 |
∵三棱锥的体积为
| 2 |
| 3 |
∴
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 2 |
| 3 |
∴a3=
| 8 |
| 27 |
∵斜高为
| ||
| 2 |
∴表面积为
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
18
| ||||
| 27 |
故答案为:
18
| ||||
| 27 |
点评:本题主要考查棱锥,线面关系、直线与平面所成的角、点到面的距离等基本知识,同时考查空间想象能力和推理、运算能力.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )
如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为( )A、14
| ||
B、6+2
| ||
C、12+2
| ||
D、16+2
|
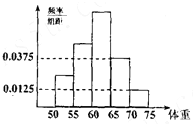 为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为
为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为 给出如图所示的数表序列.其中表i(i=1,2,3,…)有i行,表中每一个数“两脚”的两数都是此数的2倍,记表n中所有的数之和为an,例如a2=5,a3=17,a4=49,则an=
给出如图所示的数表序列.其中表i(i=1,2,3,…)有i行,表中每一个数“两脚”的两数都是此数的2倍,记表n中所有的数之和为an,例如a2=5,a3=17,a4=49,则an= 如图阴影部分是圆O的内接正方形,随机撒314粒黄豆,则预测黄豆落在正方形内的约
如图阴影部分是圆O的内接正方形,随机撒314粒黄豆,则预测黄豆落在正方形内的约