题目内容
已知递增的等差数列{an}的首项a1=1，且a1、a2、a4成等比数列．则数列{an}的通项公式为 ；则a2+a5+a8+…+a3n-1+…+a3n+8的表达式为 ．
考点：等差数列的通项公式,等差数列的前n项和
专题：等差数列与等比数列
分析：由题意易得公差d的方程，解方程可得通项公式，又可得a2+a5+a8+…+a3n-1+…+a3n+8表示2为首项3为公差的等差数列的前n+3项和，由等差数列的求和公式可得．
解答：
解：递增的等差数列{an}的公差为d，则d＞0，
∵a1、a2、a4成等比数列，∴a22=a1a4，
∴（1+d）2=1×（1+3d），解得d=1，
∴数列{an}的通项公式为：an=1+n-1=n，
∴a2+a5+a8+…+a3n-1+…+a3n+8表示2为首项3为公差的等差数列的前n+3项和，
∴a2+a5+a8+…+a3n-1+…+a3n+8=2（n+3）+
×3=
故答案为：an=n；
．
∵a1、a2、a4成等比数列，∴a22=a1a4，
∴（1+d）2=1×（1+3d），解得d=1，
∴数列{an}的通项公式为：an=1+n-1=n，
∴a2+a5+a8+…+a3n-1+…+a3n+8表示2为首项3为公差的等差数列的前n+3项和，
∴a2+a5+a8+…+a3n-1+…+a3n+8=2（n+3）+
| (n+3)(n+2) |
| 2 |
| 3n2+19n+30 |
| 2 |
故答案为：an=n；
| 3n2+19n+30 |
| 2 |
点评：本题考查等差数列的通项公式和求和公式，涉及等差数列的判定，属基础题．
练习册系列答案
相关题目
设集合A={x|
＞1}，B={y|y=2x}，x∈[-1，0]，则A∪B=（ ）
| 1 |
| x |
| A、（-∞，1] | B、（0，1） |
| C、（0，1] | D、∅ |
如图，在直三棱柱ABC-A1B1C1中，AA1=4，AB=5，BC=3，AC=4，D、E分半为CC1、AB的中点．如图，ABCD-A1B1C1D1为正方体，异面直线AD与CB1所成的角是（ ）
| A、30° | B、45° |
| C、60° | D、90° |
已知正项等比数列{an}满足S3-3a1-2a2=0，若存在两项an•am使得
=4a1，则
+
的最小值是（ ）
| aman |
| 1 |
| m |
| 4 |
| n |
| A、9 | ||
B、
| ||
C、
| ||
D、
|
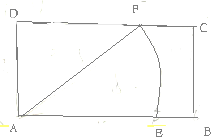如图，矩形ABCD两邻边长分别为AB=6，AD=3，以A为圆心，5为半径画圆交AB于E，交CD于F，定义点集I={P|AP≤5}