题目内容
已知三棱锥A-BCD内接于球O，AB=AD=AC=BD=
，∠BCD=60°，则球O的表面积为（ ）
| 3 |
A、
| ||
| B、2π | ||
| C、3π | ||
D、
|
考点：球的体积和表面积
专题：球
分析：画出图形，求出底面三角形的外接圆的半径，求出A到底面BCD的距离，然后取得外接球的半径，即可求解表面积．
解答：
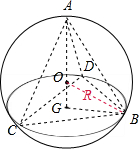解：如图：底面△BCD中，BD=
，∠BCD=60°，
∴GB=r=
=1，
∵AB=AD=AC=BD=
，A-BCD是圆锥，
∴AG⊥平面BCD，并且经过球的球心O，
则AG=
=
=
，
设球的半径为R，
OB2=OG2+GB2，即R2=(
-R)2+12，
解得R=
，
∴球O的表面积为：4πR2=4π×(
)2=
π．
故选：D．
解：如图：底面△BCD中，BD=| 3 |
∴GB=r=
| ||
| 2sin60° |
∵AB=AD=AC=BD=
| 3 |
∴AG⊥平面BCD，并且经过球的球心O，
则AG=
| AB2-GB2 |
(
|
| 2 |
设球的半径为R，
OB2=OG2+GB2，即R2=(
| 2 |
解得R=
3
| ||
| 4 |
∴球O的表面积为：4πR2=4π×(
3
| ||
| 4 |
| 9 |
| 2 |
故选：D．
点评：本题考查的表面积的求法，几何体的外接球与几何体的关系，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
已知定义在R上的奇函数f（x）满足f（x+2e）=-f（x）（其中e为自然对数的底），且在区间[e，2e]上是减函数，又a=lg6，b=log23，（
）c-2＜1且lnc＜1，则有（ ）
| 1 |
| 2 |
| A、f（a）＜f（b）＜f（c） |
| B、f（b）＜f（c）＜f（a） |
| C、f（c）＜f（a）＜f（b） |
| D、f（c）＜f（b）＜f（a） |
如果A（-3，-1）、B（2，m）、C（-8，-11）三点共线，则m的值为（ ）
| A、6 | B、7 | C、8 | D、9 |
由点P（4，3）引圆x2+y2=9的切线，则切线的长为（ ）
| A、5 | B、4 | C、3 | D、2 |
函数f（x）在x=x0处的导数可表示为y′|x=x0，即（ ）
| A、f′（x0）=f（x0+△x）-f（x0） | ||||
B、f′（x0）=
| ||||
C、f′（x0）=
| ||||
D、f′（x0）=
|
若某空间几何体的三视图如图所示，则该几何体的表面积是（ ）
| A、60 | B、54 | C、48 | D、24 |
若f（x）=x2+（2tanθ）x-1在[-1 ，
]上为减函数，则θ的取值范围是（ ）
| 3 |
A、（-
| ||||
B、[
| ||||
C、（-
| ||||
D、[
|