题目内容
平面内有n(n∈N+,n≥2)条直线,其中任何两条不平行,任何三条不过
同一点,证明:交点的个数f(n)=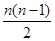 .
.
同一点,证明:交点的个数f(n)=
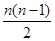 .
.见解析
(1)当n=2时,两条直线的交点只有一个,
又f(2)= ×2×(2-1)=1,
×2×(2-1)=1,
∴当n=2时,命题成立.
(2)假设n=k,∈N+,且(k>2)时,命题成立,即平面内满足题设的任何k条直线交点个数f(k)= k(k-1),
k(k-1),
那么,当n=k+1时,任取一条直线l,除l以外其他k条直线交点个数为f(k)= k(k-1),l与其他k条直线交点个数为k,从而k+1条直线共有f(k)+k个交点,
k(k-1),l与其他k条直线交点个数为k,从而k+1条直线共有f(k)+k个交点,
即f(k+1)=f(k)+k= k(k-1)+k=
k(k-1)+k= k(k-1+2)=
k(k-1+2)= k(k+1)=
k(k+1)= (k+1)[(k+1)-1],
(k+1)[(k+1)-1],
这表明,当n=k+1时,命题成立.
由(1)、(2)可知,对n∈N+(n≥2)命题都成立.
又f(2)=
 ×2×(2-1)=1,
×2×(2-1)=1,∴当n=2时,命题成立.
(2)假设n=k,∈N+,且(k>2)时,命题成立,即平面内满足题设的任何k条直线交点个数f(k)=
 k(k-1),
k(k-1),那么,当n=k+1时,任取一条直线l,除l以外其他k条直线交点个数为f(k)=
 k(k-1),l与其他k条直线交点个数为k,从而k+1条直线共有f(k)+k个交点,
k(k-1),l与其他k条直线交点个数为k,从而k+1条直线共有f(k)+k个交点,即f(k+1)=f(k)+k=
 k(k-1)+k=
k(k-1)+k= k(k-1+2)=
k(k-1+2)= k(k+1)=
k(k+1)= (k+1)[(k+1)-1],
(k+1)[(k+1)-1],这表明,当n=k+1时,命题成立.
由(1)、(2)可知,对n∈N+(n≥2)命题都成立.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目





 个等式,并猜测第
个等式,并猜测第 (
(
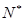 )个等式;
)个等式; +
+ +…+
+…+ =
= (n∈N*).
(n∈N*).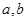 使得
使得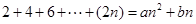 对一切
对一切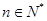 恒成立?若存在,求出
恒成立?若存在,求出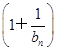 (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论. ,则n=k+1时左端在n=k时的左端加上________.
,则n=k+1时左端在n=k时的左端加上________. 对任意实数x 、y都有
对任意实数x 、y都有 ,
, 的值;
的值; ,求
,求 、
、 、
、 的值;
的值;
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。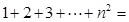
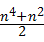 ,则当n=k+1时左端应在n=k的基础上增加 ( )
,则当n=k+1时左端应在n=k的基础上增加 ( )