题目内容
用数学归纳法证明: +
+ +…+
+…+ =
= (n∈N*).
(n∈N*).
 +
+ +…+
+…+ =
= (n∈N*).
(n∈N*).见解析
①当n=1时,左边= =
= ,右边=
,右边= =
= ,
,
左边=右边,等式成立;
②假设n=k(k≥1,k∈N*)时,等式成立,
即 +
+ +…+
+…+ =
= ,
,
当n=k+1时,左边
= +
+ +…+
+…+
+
= +
+
=
=
= ,
,
所以当n=k+1时,等式成立.
由①②可得对任意n∈N*,等式成立.
 =
= ,右边=
,右边= =
= ,
,左边=右边,等式成立;
②假设n=k(k≥1,k∈N*)时,等式成立,
即
 +
+ +…+
+…+ =
= ,
,当n=k+1时,左边
=
 +
+ +…+
+…+
+

=
 +
+
=

=

=
 ,
,所以当n=k+1时,等式成立.
由①②可得对任意n∈N*,等式成立.

练习册系列答案
相关题目
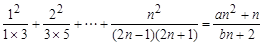 对于一切n∈N*都成立?若存在,求出a,b的值,若不存在,请说明理由。
对于一切n∈N*都成立?若存在,求出a,b的值,若不存在,请说明理由。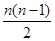 .
.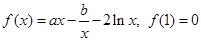
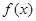 在其定义域上为单调函数,求
在其定义域上为单调函数,求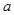 的取值范围;
的取值范围;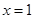 处的切线的斜率为0,
处的切线的斜率为0,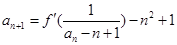 ,已知
,已知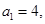 求证:
求证: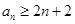
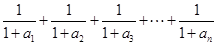 与
与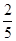 的大小,并说明理由.
的大小,并说明理由. 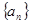 的各项均为正数,
的各项均为正数,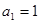 ,
,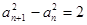
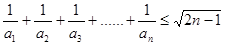 对一切
对一切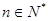 恒成立。
恒成立。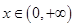 ,不等式
,不等式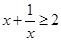 ,
,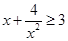 ,
,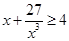 ,…,可推广为
,…,可推广为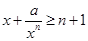 ,则
,则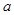 等于 .
等于 . +
+ + +
+ + (n∈N*).
(n∈N*). 时,从“
时,从“ 到
到 ”时,左边应增添的式子是( ).
”时,左边应增添的式子是( ).


