题目内容
7.已知等差数列{an}的前n项和为Sn,公差d≠0,且S1,S2,S4成等比数列.(1)求数列S1,S2,S4,…的公比q;
(2)设bn=2${\;}^{{a}_{n}}$,且S2=4,求数列{bn}的前n项和Tn.
分析 (1)设等差数列{an}的首项为a1,公差为d;从而化简可得d=2a1,从而求公比;
(2)由S2=2a1+d=4a1=4可得a1=1;从而求得bn=2${\;}^{{a}_{n}}$=22n-1=$\frac{{4}^{n}}{2}$,从而求前n项和.
解答 解:(1)设等差数列{an}的首项为a1,公差为d;
S1=a1,S2=2a1+d,S4=4a1+6d,
故(2a1+d)2=a1(4a1+6d),
故d=2a1,
故q=$\frac{{S}_{2}}{{S}_{1}}$=$\frac{4{a}_{1}}{{a}_{1}}$=4;
(2)∵S2=2a1+d=4a1=4,
∴a1=1;
∴an=1+2(n-1)=2n-1,
∴bn=2${\;}^{{a}_{n}}$=22n-1=$\frac{{4}^{n}}{2}$,
∴{bn}是以2为首项,4为公比的等比数列,
∴Tn=$\frac{2(1-{4}^{n})}{1-4}$=$\frac{2}{3}$(4n-1).
点评 本题考查了等差数列与等比数列的性质的判断与应用,同时考查了方程思想的应用.

练习册系列答案
相关题目
17.执行如图所示程序框图,则输出的n为( )


| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
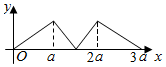
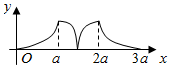
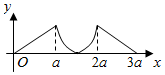
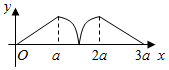
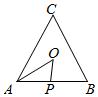 如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )
如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )