题目内容
14．$\frac{（m-1）!}{{A}_{m-1}^{n-1}•（m-n）!}$=（n-1）！．分析 由排列数公式，整体代入化简可得．
解答 解：化简可得$\frac{（m-1）!}{{A}_{m-1}^{n-1}•（m-n）!}$
=$\frac{（m-1）！}{\frac{（m-1）！}{（n-1）！•（m-n）！}•（m-n）！}$
=（n-1）！
故答案为：（n-1）！
点评 本题考查排列数公式的化简计算，属基础题．
练习册系列答案
相关题目
5．函数f（x）=3sin（ωx+φ）的部分图象如图，则f（x）的单调递增区间为（ ）
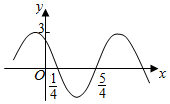
| A． | （kπ-$\frac{5}{4}$，kπ-$\frac{1}{4}$），k∈Z | B． | （2kπ-$\frac{5}{4}$，2kπ-$\frac{1}{4}$），k∈Z | ||
| C． | （2k-$\frac{5}{4}$，2k-$\frac{1}{4}$），k∈Z | D． | （k-$\frac{5}{4}$，k-$\frac{1}{4}$），k∈Z |
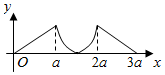
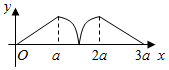
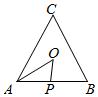如图所示，点P从点A处出发，按逆时针方向沿边长为a的正三角形ABC运动一周，O为ABC的中心，设点P走过的路程为x，△OAP的面积为f（x）（当A、O、P三点共线时，记面积为0），则函数f（x）的图象大致为（ ）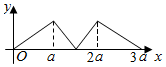
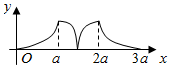
如图在正方体ABCD-A1B1C1D1中，E是棱CC1的中点．