题目内容
20.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x+2y-1=0垂直,则双曲线的离心率等于( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $\frac{\sqrt{5}}{2}$ |
分析 求出渐近线方程,由两直线垂直的条件:斜率之积为-1,可得b=2a,由a,b,c的关系和离心率公式,计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\frac{b}{a}$x,
由一条渐近线与直线x+2y-1=0垂直,可得:
-$\frac{1}{2}$•$\frac{b}{a}$=-1,即有b=2a,
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$a,
可得e=$\frac{c}{a}$=$\sqrt{5}$.
故选:B.
点评 本题考查双曲线的离心率的求法,注意运用渐近线方程和两直线垂直的条件:斜率之积为-1,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.直线l过抛物线x2=2py(p>0)的焦点,且与抛物线交于A、B两点,若线段AB的长是6,AB的中点到x轴的距离是1,则此抛物线方程是( )
| A. | x2=12y | B. | x2=8y | C. | x2=6y | D. | x2=4y |
11.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a.b>0)的右焦点与抛物线y2=2px(p>0)的焦点F重合,两条曲线在第一象限的交点为M,若MF⊥x轴,则该双曲线的离心率e=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | $\sqrt{5}$ | D. | $\sqrt{5}$-1 |
8.在正方体ABCD-A1B1C1D1中,P是A1D上的一点,且满足A1P=2PD,下列命题正确的是( )
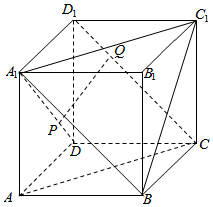

| A. | 在CD1上存在点Q,使得PQ∥平面AA1C1C | |
| B. | 在CD1上存在点Q,使得PQ⊥平面AA1C1C | |
| C. | 在CD1上存在点Q,使得PQ∥平面A1BC1 | |
| D. | 在CD1上存在点Q,使得PQ⊥平面A1BC1 |
10.对于数列{an},“an+1<|an|(n=1,2,…)”是“{an}为递减数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 必要条件 | D. | 既不充分也不必要条件 |