题目内容
12.已知函数f(x)=alnx-x+1,g(x)=-x2+(a+1)x+1,若对任意的x∈[1,e],不等式f(x)≥g(x)恒成立,求实数a的取值范围.分析 不等式可化为a(lnx-x)≥-x2+2x,根据条件可知lnx-x<0,可得a≤$\frac{{x}^{2}-2x}{x-lnx}$,把恒成立问题转换为最值问题,只需求出右式的最小值即可,
利用构造函数,通过导函数求出函数的单调性,确定函数的最值.
解答 解:对任意的x∈[1,e],不等式f(x)≥g(x)恒成立,
∴alnx-x+1≥-x2+(a+1)x+1,
∴a(lnx-x)≥-x2+2x,
∵x∈[1,e],
∴lnx<1<x,
∴a≤$\frac{{x}^{2}-2x}{x-lnx}$,
设t(x)=$\frac{{x}^{2}-2x}{x-lnx}$,x∈[1,e],
求导,得t′(x)=
$\frac{(x-1)(x+2-lnx)}{(x-lnx)^{2}}$,
∵x∈[1,e],x-1≥0,lnx≤1,x+2-lnx>0,
从而t′(x)≥0,t(x)在[1,e]上为增函数.
所以t(x)min=t(1)=-1,所以a≤-1.
故答案为a≤-1.
点评 考查了恒成立问题的转换思想和利用导函数判断函数的单调性,根据单调性求函数的最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3. 如图,四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$,二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,则异面直线EF与AC所成的角的余弦值是( )
如图,四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$,二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,则异面直线EF与AC所成的角的余弦值是( )
 如图,四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$,二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,则异面直线EF与AC所成的角的余弦值是( )
如图,四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$,二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,则异面直线EF与AC所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
20.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x+2y-1=0垂直,则双曲线的离心率等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $\frac{\sqrt{5}}{2}$ |
4.已知m,n∈R,则“mn>0”是“一次函数y=$\frac{m}{n}x$+$\frac{1}{n}$的图象不经过第二象限”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 在三棱锥A-BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2$\sqrt{3}$,AC=$\sqrt{6}$.
在三棱锥A-BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2$\sqrt{3}$,AC=$\sqrt{6}$.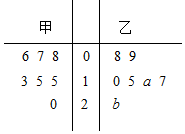 甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.