题目内容
已知双曲线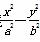 =1(a>0,b>0)的右焦点为F(c,0).
=1(a>0,b>0)的右焦点为F(c,0).
(1)若双曲线的一条渐近线方程为y=x且c=2,求双曲线的方程;
(2)以原点O为圆心,c为半径作圆,该圆与双曲线在第一象限的交点为A,过A作圆的切线,斜率为- ,求双曲线的离心率.
,求双曲线的离心率.
解析: (1)∵双曲线的渐近线为y=±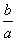 x,∴a=b,
x,∴a=b,
∴c2=a2+b2=2a2=4,∴a2=b2=2,
∴双曲线方程为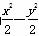 =1.
=1.
(2)设点A的坐标为(x0,y0),
∴直线AO的斜率满足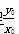 ·(-
·(- )=-1,
)=-1,
∴x0= y0.①
y0.①
依题意,圆的方程为x2+y2=c2,
将①代入圆的方程得3y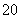 +y
+y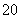 =c2,即y0=
=c2,即y0= c,
c,
∴x0=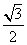 c,
c,
∴点A的坐标为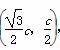 ,代入双曲线方程得
,代入双曲线方程得
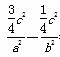 =1,即
=1,即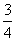 b2c2-
b2c2- a2c2=a2b2,②
a2c2=a2b2,②
又∵a2+b2=c2,∴将b2=c2-a2代入②式,整理得
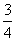 c44-2a2c2+a4=0,
c44-2a2c2+a4=0,
∴3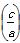 -8
-8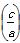 2+4=0,
2+4=0,
∴(3e2-2)(e2-2)=0,∵e>1,∴e= ,
,
∴双曲线的离心率为 .
.

练习册系列答案
相关题目

 =________.
=________. 的点的个数是________.
的点的个数是________. ,求证:a>b.
,求证:a>b. ≥
≥ .
.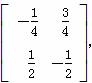 ,求矩阵A的特征值.
,求矩阵A的特征值.