题目内容
12.已知函数f(x)=ax2+bx+c(a≠0)是偶函数,则函数g(x)=ax3+bx2+cx是( )| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
分析 由f(x)=ax2+bx+c是偶函数,则有f(-x)=f(x),求得b=0.可得g(x)=ax3 +cx,故有g(-x)=-g(x),可得函数g(x)为奇函数.
解答 解:若f(x)=ax2+bx+c是偶函数,则有f(-x)=f(x),即 ax2+bx+c=ax2-bx+c,∴b=0.
故g(x)=ax3+bx2+cx=ax3 +cx,故有g(-x)=a(-x)3+c(-x)=-(ax3+cx)=-g(x),
故函数g(x)为奇函数,
故选:A.
点评 本题主要考查偶函数的定义.函数的奇偶性的判断,属于中档题.

练习册系列答案
相关题目
14.已知正三角形ABC的顶点A,B在抛物线y2=4x上,另一个顶点C(4,0),则这样的正三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
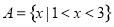 ,集合
,集合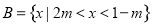 .
.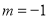 时,求
时,求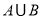 ;
;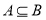 ,求实数
,求实数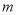 的取值范围;
的取值范围;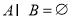 ,求实数
,求实数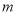 的取值范围.
的取值范围. ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 如图,四边形ABCD为矩形,点E,F在以O为圆心以AB为直径的圆上,AB∥EF,平面ABCD⊥平面ABEF,BC=EF=$\frac{1}{2}$AB.
如图,四边形ABCD为矩形,点E,F在以O为圆心以AB为直径的圆上,AB∥EF,平面ABCD⊥平面ABEF,BC=EF=$\frac{1}{2}$AB.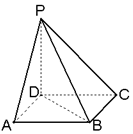 如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.
如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.