题目内容
1.已知点P(x,y)的坐标满足$\left\{\begin{array}{l}{x≤0}\\{y>x}\\{y<2x+1}\end{array}\right.$,则$\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}$的取值范围为(-$\sqrt{2}$,1].分析 由约束条件作出可行域,设A(1,1),P(x,y)为可行域内的一动点,向量$\overrightarrow{OA}$、$\overrightarrow{OP}$的夹角为θ,可得cosθ=$\frac{\sqrt{2}}{2}•$$\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}$,再由θ的范围求得cosθ的范围,则答案可求.
解答 解:由约束条件$\left\{\begin{array}{l}{x≤0}\\{y>x}\\{y<2x+1}\end{array}\right.$作出可行域如图,
设A(1,1),P(x,y)为可行域内的一动点,
向量$\overrightarrow{OA}$、$\overrightarrow{OP}$的夹角为θ,
∵|$\overrightarrow{OP}$|=$\sqrt{{x}^{2}{+y}^{2}}$,$\overrightarrow{OA}•\overrightarrow{OP}=x+y$,
∴cosθ=$\frac{\overrightarrow{OA}•\overrightarrow{OP}}{|\overrightarrow{OA}||\overrightarrow{OP}|}$=$\frac{x+y}{\sqrt{2}•\sqrt{{x}^{2}+{y}^{2}}}=\frac{\sqrt{2}}{2}•\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}$.
∵当P运动到B时,θ有最小值$\frac{π}{4}$,当P运动到C时,θ有最大值π,
∴-1<cosθ≤$\frac{\sqrt{2}}{2}$,即-1<$\frac{\sqrt{2}}{2}•\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}≤\frac{\sqrt{2}}{2}$,
则$-\sqrt{2}$<$\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}$≤1.
∴$\frac{x+y}{\sqrt{{x}^{2}+{y}^{2}}}$的取值范围为(-$\sqrt{2}$,1].
故答案为:(-$\sqrt{2}$,1].
点评 本题考查简单的线性规划,考查数形结合的解题思想方法与数学转化思想方法,是中档题.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
| A. | 5p | B. | 10p | C. | 11p | D. | 12p |
| A. | $(0,\frac{2}{5}]$ | B. | $(0,\frac{2}{3}]$ | C. | (0,1] | D. | (0,2] |
| A. | 5 | B. | $\frac{11}{5}$ | C. | $\frac{9}{5}$ | D. | $\frac{7}{5}$ |
 B.
B.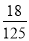
 D.
D.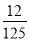
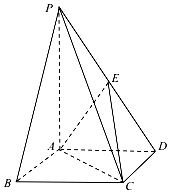 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.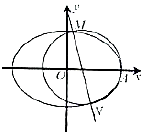 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,E的右焦点到直线y=x+1的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,E的右焦点到直线y=x+1的距离为$\sqrt{2}$.