题目内容
4. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求二面角B-PD-C的余弦值.
分析 (Ⅰ)证明CD⊥PA,BC⊥PA.即可得 PA⊥平面ABCD.
(Ⅱ) 分别以AD,AB,AP所在的直线分别为x,y,z轴,建立如图空间直角坐标系,
求出平面PDC的一个法向量、平面PDB的一个法向量即可.
解答 解:(1)证明:在正方形ABCD中,CD⊥AD.
因为CD⊥PD,AD∩PD=D,
所以 CD⊥平面PAD. 因为 PA?平面PAD,
所以 CD⊥PA. 同理,BC⊥PA.因为 BC∩CD=C,
所以 PA⊥平面ABCD. …(5分)
(Ⅱ)解:连接AC,由(Ⅰ)知PA⊥平面ABCD.
因为AC?平面ABCD,所以PA⊥AC.
因为PC=$\sqrt{3}$,AC=$\sqrt{2}$,所以PA=1.
分别以AD,AB,AP所在的直线分别为x,y,z轴,建立如图空间直角坐标系,
由题意可得:B(0,1,0),D(1,0,0),C(1,1,0),P(0,0,1). …(6分)
所以$\overrightarrow{DC}=(0,1,0)$,$\overrightarrow{DP}=(-1,0,1)$,$\overrightarrow{BD}=(1,-1,0)$,$\overrightarrow{DP}=(0,-1,1)$.
设平面PDC的一个法向量$\overrightarrow{m}=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DC}=y=0}\\{\overrightarrow{m}•\overrightarrow{DP}=-x+z=0}\end{array}\right.$ 即 令x=1,得z=1.
所以$\overrightarrow{m}=(1,0,1)$. …(8分)
同理可求:平面PDB的一个法向量$\overrightarrow{n}=(1,1,1)$. …(10分)
所以cos$<\overrightarrow{m},\overrightarrow{n}>=\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{\sqrt{6}}{3}$.
所以二面角B-PD-C的余弦值为$\frac{\sqrt{6}}{3}$. …(12分)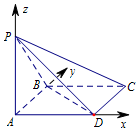
点评 本题考查了空间线面垂直的判定,向量法求二面角,属于中档题.

 天天练口算系列答案
天天练口算系列答案| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{5}$ | C. | 2+2$\sqrt{3}$ | D. | $\sqrt{7}$+1 |
| A. | 5p | B. | 10p | C. | 11p | D. | 12p |
 在
在 上单调递增,且函数
上单调递增,且函数 是偶函数,则下列结论成立的是( )
是偶函数,则下列结论成立的是( ) B.
B.
 D.
D.
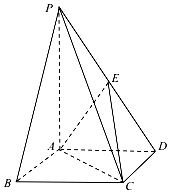 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.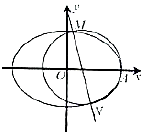 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,E的右焦点到直线y=x+1的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,E的右焦点到直线y=x+1的距离为$\sqrt{2}$.