题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{|{2}^{x}-1|,x<2}\\{\frac{3}{x-1},x≥2}\end{array}\right.$若方程f(x)=a有三个不同的实数根,则实数a的取值范围是( )| A. | (1,3) | B. | (0,3) | C. | (0,2) | D. | (0,1) |
分析 结合方程f(x)=a有三个不同的实数解,将问题转化为函数图象交点的个数判断问题,进而结合函数f(x)的图象即可获得解答.
解答 解:由题意可知:函数f(x)的图象如下:
由关于x的方程f(x)-a=0有三个不同的实数解,
可知函数y=a与函数y=f(x)有三个不同的交点,
由图象易知:实数a的取值范围为(0,1),
故选:D.
点评 此题考查的是方程的根的存在性以及根的个数问题.在解答的过程当中充分体现了问题转化的思想、数形结合的思想.

练习册系列答案
相关题目
12.已知a,b∈R,则“a>0”是“a+b2>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.如果$\frac{1-cosα}{sinα}=\frac{1}{2}$,那么sinα+cosα的值是( )
| A. | $\frac{7}{5}$ | B. | $\frac{8}{5}$ | C. | 1 | D. | $\frac{29}{15}$ |
1.与35°角的终边相同的角是( )
| A. | -35°+k•360°,k∈Z | B. | -325°+k•360°,k∈Z | ||
| C. | 325°+k•360°,k∈Z | D. | 35°+(2k+1)×180°,k∈Z |
 是函数
是函数 定义域内的一个区间,若存在
定义域内的一个区间,若存在 ,使得
,使得 ,则称
,则称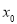 是
是 的一个“次不动点”,也称
的一个“次不动点”,也称 在区间
在区间 上存在次不动点.若函数
上存在次不动点.若函数 在区间
在区间 上存在次不动点,则实数
上存在次不动点,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.


 ,求
,求 的分布列及数学期望.
的分布列及数学期望.