题目内容
3.若实数x,y满足不等式组$\left\{\begin{array}{l}{3x+y-8≤0}\\{x+2y-1≥0}\\{2x-y-2≥0}\end{array}\right.$,则x2+y2的最大值为( )| A. | 8 | B. | 10 | C. | 2$\sqrt{2}$ | D. | $\sqrt{10}$ |
分析 作出平面区域,则x2+y2表示平面区域内的点到原点的最大距离的平方.
解答 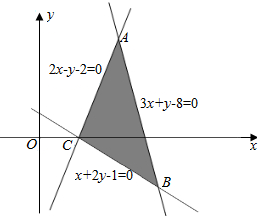 解:作出平面区域如图:
解:作出平面区域如图:
解方程组$\left\{\begin{array}{l}{2x-y-2=0}\\{3x+y-8=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,∴A(2,2).∴|OA|2=22+22=8.
解方程组$\left\{\begin{array}{l}{x+2y-1=0}\\{3x+y-8=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,∴B(3,-1).∴|OB|2=32+(-1)2=10.
∴平面区域内的B点到原点得距离最大.
∴x2+y2的最大值是10.
故选:B.
点评 本题考查了简单的线性规划,弄清x2+y2的几何意义是解题关键,属于基础题.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
11.已知a>0,b>0,且$\frac{1}{a}+\frac{1}{b}=1$,则a+4b的最小值为( )
| A. | 4 | B. | 9 | C. | 10 | D. | 12 |