题目内容
已知等差数列{an}和{bn}的前n项和分别为Sn，Tn，且
=
对任意n∈N*恒成立，则
的值为 ．
| Sn |
| Tn |
| 2n |
| n+2 |
| a10 |
| b10 |
考点：数列的求和
专题：等差数列与等比数列
分析：
=
=
=
，由此能求出结果．
| a10 |
| b10 |
| 2a10 |
| 2b10 |
| ||
|
| S19 |
| T19 |
解答：
解：∵等差数列{an}和{bn}的前n项和分别为Sn，Tn，
且
=
对任意n∈N*恒成立，
∴
=
=
=
=
=
=
．
故答案为：
．
且
| Sn |
| Tn |
| 2n |
| n+2 |
∴
| a10 |
| b10 |
| 2a10 |
| 2b10 |
| a1+a19 |
| b1+b19 |
=
| ||
|
=
| S19 |
| T19 |
| 2×19 |
| 19+2 |
| 38 |
| 21 |
故答案为：
| 38 |
| 21 |
点评：本题考查两个数列的第10项的比值的求法，是中档题，解题时要认真审题，注意等差数列的通项公式的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
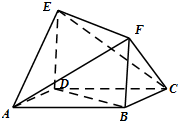如图所示的多面体中，ABCD是菱形，BDEF是矩形，ED⊥面ABCD，