题目内容
如图,三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是以
是以![]() 为底边的等腰三角形,平面
为底边的等腰三角形,平面![]() 平面
平面![]() ,
,![]() 分别为棱
分别为棱![]() 、
、![]() 的中点
的中点
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 为整数,且
为整数,且![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
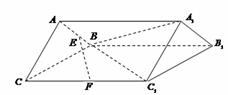
 解(1)
解(1)![]() ,
,![]() 是以
是以![]() 为斜边的等腰直角三角形, 取
为斜边的等腰直角三角形, 取![]() 的中点
的中点![]() ,连接
,连接![]() ,设
,设![]() ,则
,则![]()
![]() 面
面![]() 面
面![]() ,且面
,且面![]() 面
面![]() ,
,
![]() 面
面![]() ,
,![]() 面
面![]()
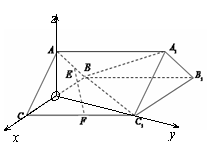
以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系
![]()
![]()
![]() 设平面
设平面![]() 的一个法向量为
的一个法向量为![]()
![]()
![]() , 又
, 又![]() 面
面![]()
![]() 面
面![]()
(2)设平面![]() 的一个法向量为
的一个法向量为![]() 又
又![]()
则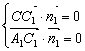 ,
,![]() ,令
,令![]() ,则
,则![]()
又![]()
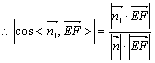 =
=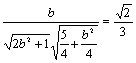
解得![]() 或
或![]() ,
, ![]() 为整数
为整数 ![]()
所以![]() 同理可求得平面
同理可求得平面![]() 的一个法向量
的一个法向量![]()
![]() =
=![]()
又二面角![]() 为锐二面角,故余弦值为
为锐二面角,故余弦值为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
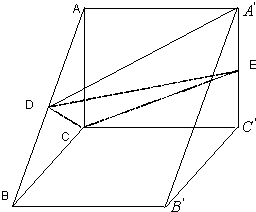 如图,三棱柱中,平面AC′⊥面BB′C′C,∠CC′B′=60°,BC=CC′AC=2,点D、E分别为棱AB,A′C′的中点
如图,三棱柱中,平面AC′⊥面BB′C′C,∠CC′B′=60°,BC=CC′AC=2,点D、E分别为棱AB,A′C′的中点
 中,侧面
中,侧面
 底面
底面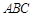 ,
,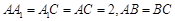 ,且
,且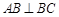 ,O为
,O为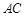 中点.
中点.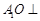 平面
平面 与平面
与平面 所成角的正弦值
所成角的正弦值
 中,
中, ⊥面
⊥面 ,
, ,
, ,
, 为
为 的中点.
的中点. ;
; 的余弦值;
的余弦值; ,使得
,使得 ?请证明你的结论.
?请证明你的结论.
 中,
中,  底面
底面 ,
, ,
,  ,
, , 点D是
, 点D是 的中点.
的中点.
 ; (Ⅱ)
求证
; (Ⅱ)
求证 ∥平面
∥平面
 .
.