题目内容
某射击手每次命中目标的概率为
,求X的概率分布和数学期望.
(1)连续射击3次,击中目标的次数为X;
(2)只有3发子弹,击中目标或子弹打完就停止射击,耗用子弹数X.
| 2 |
| 3 |
(1)连续射击3次,击中目标的次数为X;
(2)只有3发子弹,击中目标或子弹打完就停止射击,耗用子弹数X.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)由题意知X=0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望.
(2)由题意知X=1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望.
(2)由题意知X=1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答:
解:(1)由题意知X=0,1,2,3,
P(X=0)=(1-
)3=
,
P(X=1)=
(
)(1-
)2=
,
P(X=2)=
(
)2(1-
)=
,
P(X=3)=(
)3=
,
∴X的分布列为:
EX=0×
+1×
+2×
+3×
=2.
(2)由题意知X=1,2,3,
P(X=1)=
,
P(X=2)=
×
=
,
P(X=3)=
×
=
,
∴X的分布列为:
∴E(X)=1×
+2×
+3×
=
.
P(X=0)=(1-
| 2 |
| 3 |
| 1 |
| 27 |
P(X=1)=
| C | 1 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 6 |
| 27 |
P(X=2)=
| C | 2 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 12 |
| 27 |
P(X=3)=(
| 2 |
| 3 |
| 8 |
| 27 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 27 |
| 6 |
| 27 |
| 12 |
| 27 |
| 8 |
| 27 |
(2)由题意知X=1,2,3,
P(X=1)=
| 2 |
| 3 |
P(X=2)=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
P(X=3)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
∴X的分布列为:
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 9 |
| 13 |
| 9 |
点评:本题考查离散型随机变量的分布列、数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知sin
+cos
=
,则cos2θ=( )
| θ |
| 2 |
| θ |
| 2 |
| 1 |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
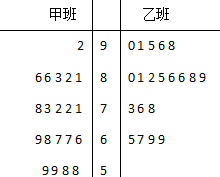 我市某校某数学老师这学期分别用m,n两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如图所示.
我市某校某数学老师这学期分别用m,n两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如图所示.