题目内容
8．已知集合A={x|$\frac{x-3}{x+1}$≥0}，B={x|log2x＜2}，则（∁RA）∩B=（ ）| A． | （0，3） | B． | （0，3] | C． | [-1，4] | D． | [-1，4） |
分析 求出集合A，B，利用集合的基本运算即可的结论．
解答 解：集合A={x|$\frac{x-3}{x+1}$≥0}=（-∞，-1）∪[3，+∞），
∴（∁RA）=[-1，3）
B={x|log2x＜2}，
∴$\left\{\begin{array}{l}{x＞0}\\{x＜4}\end{array}\right.$，
∴B=（0，4），
∴（∁RA）∩B=（0，3）．
故选：A．
点评 本题考查不等式的解集及其集合间的运算．比较基础．
练习册系列答案
相关题目
8．一个几何体的三视图如图所示，则这个几何体的体积为（ ）
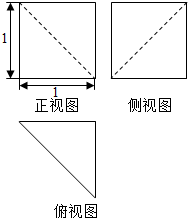
| A． | $\frac{5}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |
