题目内容
已知数列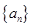
是首项为
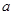且公比q不等于1的等比数列，
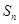是其前n项的和，
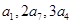成等差数列.证明：
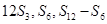成等比数列.
要证明三项是成等差，只要利用等差中项的性质分析求解可得。
解析试题分析：证明：由
成等差数列， 得
，
即 
变形得 
所以
（舍去）.
由 
得 
所以
成等比数列.
考点：等比数列的定义，等差数列
点评：考查了等差数列和等比数列的定义和通项公式的运用，属于基础题。
练习册系列答案
相关题目
题目内容
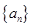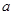已知数列是首项为且公比q不等于1的等比数列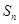，是其前n项的和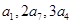，成等差数列.证明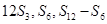：成等比数列.
要证明三项是成等差，只要利用等差中项的性质分析求解可得。
解析试题分析：证明：由成等差数列， 得，
即 变形得
所以（舍去）.
由
得 所以成等比数列.
考点：等比数列的定义，等差数列
点评：考查了等差数列和等比数列的定义和通项公式的运用，属于基础题。
中，
是数列
的前
项和，对任意
，有
.函数
，数列
的首项
求证：
是等比数列并求
，
，求数列
的前n项和
.
的前n项和
（n为正整数）．
，求证数列
是等差数列；
，
。是否存在最小的正整数
，使得对于
都有
恒成立，若存在，求出
中，
，求其第4项及前5项和. 
}中
，求证数列{
}是等比数列；
的各项均为正数，且
求数列
的前
项和
.
}的前n项和为
， 已知对任意的
，点
，均在函数
且
均为常数)的图像上.
求数列
的前
项和
的前
项和为
，
，
，求数列
中，
，公比
，且
，
是
与
的等比中项。设
．
的通项公式；
项和为
,
，求
．