题目内容
(本小题满分12分)
等比数列{ }的前n项和为
}的前n项和为 , 已知对任意的
, 已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(2)当b=2时,记  求数列
求数列 的前
的前 项和
项和
(1) (2)
(2) 
解析试题分析:解:因为对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.所以得
均为常数)的图像上.所以得 ,
,
当 时,
时, ,
,
当 时,
时, ,
,
又因为{ }为等比数列, 所以
}为等比数列, 所以 , 公比为
, 公比为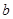 , 所以
, 所以
(2)当b=2时, ,
, 
则

相减,得


所以
考点:数列的知识
点评:解决该试题的关键是利用通项公式来选择求和方法一般要掌握的是错位相减法和裂项求和以及分组求和,属于基础题。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
数列 ,…前n项的和为
,…前n项的和为
A. | B. |
C. | D. |
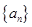 中,
中, ,
,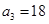 ,等差数列
,等差数列 中,
中, ,且
,且 。
。 ;(2)求数列
;(2)求数列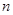 项和
项和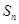 。
。 是等比数列,且
是等比数列,且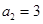 ,
,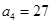
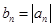 ,求
,求 的前
的前 项的和
项的和
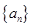 是首项为
是首项为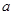 且公比q不等于1的等比数列,
且公比q不等于1的等比数列,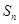 是其前n项的和,
是其前n项的和,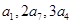 成等差数列.证明:
成等差数列.证明: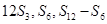 成等比数列.
成等比数列. }满足
}满足 。
。 }是等比数列。
}是等比数列。 项的和为
项的和为  的值。
的值。 满足:
满足:
 为等比数列;
为等比数列; 为递增数列;
为递增数列; 的取值范围。
的取值范围。 中,
中,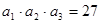 ,
,
 (2)求出
(2)求出