题目内容

1．在△ABC中，$tanA=\frac{1}{2}，cosB=\frac{{3\sqrt{10}}}{10}$，则tanC的值是（　　）
A．1B．-1C．2D．-2

分析 先通过cosB，求得sinB，进而可求得tanB，进而根据tanC=-tan（A+B），利用正切的两角和公式求得答案．

解答 解：∵cosB=$\frac{3\sqrt{10}}{10}$，
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{10}}{10}$，tanB=$\frac{sinB}{cosB}$=$\frac{1}{3}$，
∴tanC=-tan（A+B）=-$\frac{tanA+tanB}{1-tanAtanB}$=-1．
故选：B．

点评 本题主要考查了同角三角函数基本关系的应用．当进行三角关系变换的时候，要特别注意函数值的正负．

练习册系列答案
相关题目
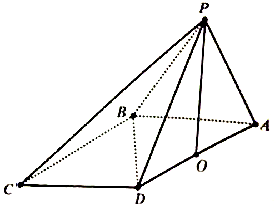11．在四棱锥P-ABCD中，$∠DBA=\frac{π}{2}$，$AB\underline{\underline∥}CD$，△PAB和△PBD都是边长为2的等边三角形，设P在底面ABCD的射影为O．
（1）求证：O是AD中点；
（2）证明：BC⊥PB；
（3）求点A到面PBC的距离．
12．如图，在三棱柱ABC-A1B1C1中，AB⊥平面BB1C1C，且四边形BB1C1C是菱形，∠BCC1=60°．
（1）求证：AC1⊥B1C；
（2）若AC⊥AB1，三棱锥A-BB1C的体积为$\frac{\sqrt{6}}{3}$，求△ABC的面积．
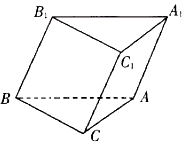9．如图，斜三棱柱ABC-A1B1C1的底面是直角三角形，∠ACB=90°，点B1在底面内的射影恰好是BC的中点，且BC=CA=2．
（1）求证：平面ACC1A1⊥平面B1C1CB；
（2）若二面角B-AB1-C1的余弦值为$-\frac{5}{7}$，求斜三棱柱ABC-A1B1C1的高．
16．椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点分别为F1，F2，点P在椭圆C上，满足$\overrightarrow{P{F_1}}•\overrightarrow{{F_1}{F_2}}=0，|{\overrightarrow{P{F_1}}}|=\frac{{\sqrt{5}}}{5}，|{\overrightarrow{P{F_2}}}|=\frac{{9\sqrt{5}}}{5}$．
（1）求椭圆C的方程．
（2）设O为坐标原点，过椭圆C的左焦点F1的动直线l与椭圆C相交于M，N两点，是否存在常数t，使得$\overrightarrow{OM}•\overrightarrow{ON}+t\overrightarrow{{F_1}M}•\overrightarrow{{F_1}N}$为定值，若存在，求t的值；若不存在，请说明理由．
6．在如图所示的几何体中，平面ADNM⊥平面ABCD，四边形ABCD是菱形，ADNM是矩形，$∠DAB=\frac{π}{3}$，AB=2，AM=1，E是AB的中点．
（1）求证：平面DEM⊥平面ABM；
（2）在线段AM上是否存在点P，使二面角P-EC-D的大小为$\frac{π}{4}$？若存在，求出AP的长；若不存在，请说明理由．
13．已知数列{an}满足${a_1}=\frac{3}{2}$，an+1=3an-1（n∈N+）．
（1）若数列{bn}满足${b_n}={a_n}-\frac{1}{2}$，求证：{bn}是等比数列；
（2）若数列{cn}满足cn=log3an，Tn=c1+c2+…+cn，求证：${T_n}＞\frac{n（n-1）}{2}$．
10．已知数列{an}中，a3=5，a2+a6=14，且2${\;}^{{a}_{n}}$，2${\;}^{{a}_{n+1}}$，2${\;}^{{a}_{n+2}}$成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足bn=an-（-1）nn，数列{bn}的前n项和为Tn，求T21．
11．已知抛物线y2=8x的准线过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一个焦点，则当$\frac{4}{a^2}+\frac{1}{b^2}$取得最小值时，双曲线的离心率为$\frac{\sqrt{6}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网