题目内容
12. 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,且四边形BB1C1C是菱形,∠BCC1=60°.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,且四边形BB1C1C是菱形,∠BCC1=60°.(1)求证:AC1⊥B1C;
(2)若AC⊥AB1,三棱锥A-BB1C的体积为$\frac{\sqrt{6}}{3}$,求△ABC的面积.
分析 (1)连结BC1,推导出AB⊥B1C,B1C⊥BC1,从而B1C⊥平面ABC1,由此能求出AC1⊥B1C.
(2)由AB⊥平面BB1C1C,BC=BB1,知AC=AB1,由三棱锥A-BB1C的体积为$\frac{\sqrt{6}}{3}$,求出菱形BB1C1C的边长,由此能求出△ABC的面积.
解答 证明:(1)连结BC1,
∵AB⊥平面BB1C1C,B1C?平面BB1C1C,∴AB⊥B1C,
∵四边形BB1C1C是菱形,∴B1C⊥BC1,
∵AB∩BC1=B,∴B1C⊥平面ABC1,
∵AC1?平面ABC1,∴AC1⊥B1C.
解:(2)由AB⊥平面BB1C1C,BC=BB1,知AC=AB1,
设菱形BB1C1C的边长为a,
∵∠BCC1=60°,∴${B}_{1}{C}^{2}$=$B{C}^{2}+B{{B}_{1}}^{2}-2BC•B{B}_{1}•cos120°$=3a2,
∵AC⊥AB1,∴$A{C}^{2}+A{{B}_{1}}^{2}={B}_{1}{C}^{2}=3{a}^{2}$,∴AC=AB1=$\frac{\sqrt{6}}{2}$a,
∵AB⊥侧面BB1C1C,BC?侧面BB1C1C,∴AB⊥BC,
∴在Rt△ABC中,AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\frac{\sqrt{2}}{2}a$,
∵三棱锥A-BB1C的体积为$\frac{\sqrt{6}}{3}$,
∴${V}_{A-B{B}_{1}C}=\frac{1}{3}{S}_{△B{B}_{1}C}•AB=\frac{1}{3}×\frac{1}{2}×a×a×sin120°$×$\frac{\sqrt{2}}{2}a=\frac{\sqrt{6}}{3}$,
解得a=2,∴AB=$\frac{\sqrt{2}}{2}a=\sqrt{2}$,BC=a=2,
∴△ABC的面积S△ABC=$\frac{1}{2}$×BC×AB=$\frac{1}{2}×2×\sqrt{2}$=$\sqrt{2}$.
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法及应用,是中档题,解题时要认真审题,注意空间思维能力的培养.


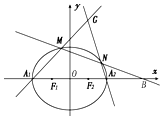 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点. 如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.
如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.