题目内容
12.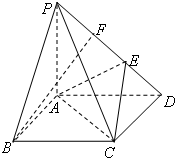 四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=$\sqrt{2}$,E,F为PD上两点,且PF=ED=$\frac{1}{3}$PD.
四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=$\sqrt{2}$,E,F为PD上两点,且PF=ED=$\frac{1}{3}$PD.(1)求证:BF∥面ACE;
(2)求异面直线PC与AE所成角的余弦值;
(3)求二面角P-AC-E的余弦值.
分析 (1)连接BD交AC与O,连接OE,可得EO∥BF,进而由线面垂直的判定定理可得:BF∥面ACE;
(2)以A为坐标原点,AB,AD,AP分别为x,y,z轴正方向建立空间坐标系数O-xyz,求出直线PC与AE的方向向量,代入夹角公式,可得异面直线PC与AE所成角的余弦值;
(3)求出平面PAC和ACE的法向量,代入向量夹角公式,可得二面角P-AC-E的余弦值.
解答 证明:(1)连接BD交AC与O,连接OE,
∵PF=ED=$\frac{1}{3}$PD.
∴ED=FE,
∴EO∥BF,
∵EO?面ACE,BF?面ACE;
∴BF∥面ACE;
解:(2)以A为坐标原点,AB,AD,AP分别为x,y,z轴正方向建立空间坐标系数O-xyz,
则B(1,0,0),D(0,1,0),P(0,0,1),C(1,1,0),F(0,$\frac{1}{3}$,$\frac{2}{3}$),E(0,$\frac{2}{3}$,$\frac{1}{3}$),
则$\overrightarrow{CP}$=(-1,-1,1),$\overrightarrow{AE}$=(0,$\frac{2}{3}$,$\frac{1}{3}$),
设异面直线PC与AE所成角为θ,
则cosθ=$\frac{|\overrightarrow{CP}•\overrightarrow{AE}|}{\left|\overrightarrow{CP}\right|•\left|\overrightarrow{AE}\right|}$=$\frac{\sqrt{15}}{15}$,
(3)设平面ACE的法向量$\overrightarrow{m}$=(a,b,c),
由$\left\{\begin{array}{l}\overrightarrow{m}•\overrightarrow{AC}=0\\ \overrightarrow{m}•\overrightarrow{AE}=0\end{array}\right.$得:$\left\{\begin{array}{l}a+b=0\\ \frac{2}{3}b+\frac{1}{3}c=0\end{array}\right.$,
令a=1,则$\overrightarrow{m}$=(1,-1,2),
∵DB⊥平面PAC,
∴$\overrightarrow{DB}$=(1,-1,0)即为平面PAC的一个法向量,
故锐二面角P-AC-E的余弦值cosα=$\frac{|\overrightarrow{m}•\overrightarrow{DB}|}{\left|\overrightarrow{m}\right|•\left|\overrightarrow{DB}\right|}$=$\frac{\sqrt{3}}{3}$
点评 本题考查的知识点是线面平行的判定定理,直线与平面的夹角,二面角的平面角,难度中档.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{40}{3}$ | B. | $\frac{50}{3}$ | C. | 10 | D. | 20 |