题目内容

20．已知关于x的不等式|x+1|+|x|≥k恒成立，则实数k的取值范围是（-∞，1]．

分析 根据绝对值的意义：|x+1|+|x|表示数轴上的x对应点到-1和0对应点的距离之和，它的最小值等于1，可得答案．

解答 解：|x+1|+|x|表示数轴上的x对应点到-1和0对应点的距离之和，它的最小值等于1，
由关于x的不等式|x+1|+|x|≥k恒成立知，k≤1．
故答案为：（-∞，1]．

点评 本题考查绝对值的意义，绝对值不等式的解法，求出|x+1|+|x|的最小值，是解题的关键．

练习册系列答案
相关题目
10．若函数f（x）=2cos2x+asinx-4在$[{\frac{π}{6}，\frac{π}{2}}]$内的图象恒在x轴下方，则a的取值范围为a＜4$\sqrt{2}$．
11．已知函数f（x）=x2+（m+1）x+（m+1）的图象与x轴有公共点，则m的取值范围是（-∞，-1]∪[3，+∞）（用区间表示）．
8．已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点分别为A1，A2．，A1关于直线bx+ay=0的对称点在圆（x+a）2+y2=a2上，则椭圆的离心率为$\frac{\sqrt{2}}{2}$．
15．若关于x的一元二次方程3x2+2ax+1=0没有实数根，则a的取值范围是（　　）
A．（-∞，-$\sqrt{3}$）∪（$\sqrt{3}$，+∞）B．（-$\sqrt{3}$，$\sqrt{3}$）C．[-$\sqrt{3}$，$\sqrt{3}$]D．[-3，3]
5．已知函数f（x）=ax2-lnx（a∈R）
（1）当a=1时，求函数y=f（x）的单调区间；
（2）若?x∈（0，1]，|f（x）|≥1恒成立，求a的取值范围；
（3）若a=$\frac{e}{2}$，证明：ex-1f（x）≥x．
12．对于在区间[m，n]上有意义的两个函数f（x）与g（x），如果对任意x∈[m，n]均有|f（x）-g（x）|≤1，则称f（x）与g（x）在[m，n]上是接近的；否则称f（x）与g（x）在[m，n]上是非接近的．现有两个函数f1（x）=loga（x-3a），与f2（x）=loga$\frac{1}{x-a}$（a＞0，a≠1），给定区间[a+2，a+3]．
（1）若f1（x）与f1（x）在给定区间[a+2，a+3]上都有意义，求a的取值范围；
（2）讨论f1（x）与f1（x）在给定区间[a+2，a+3]上是否是接近的？
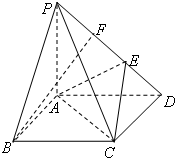12．四棱锥P-ABCD的底面是边长为1的正方形，PA⊥CD，PA=1，PD=$\sqrt{2}$，E，F为PD上两点，且PF=ED=$\frac{1}{3}$PD．
（1）求证：BF∥面ACE；
（2）求异面直线PC与AE所成角的余弦值；
（3）求二面角P-AC-E的余弦值．
13．设函数f（x）=2cos2x+$\sqrt{3}$sin2x．
（1）求函数f（x）的最小正周期和单调递增区间；
（2）求函数f（x）的最小值及x的取值集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网