题目内容
2.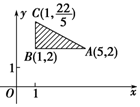 如图所示的坐标平面的可行域内(包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )
如图所示的坐标平面的可行域内(包括边界),若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{5}{3}$ |
分析 化目标函数为直线方程的斜截式,结合使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,可知直线y=-ax+z与图中AC边所在直线重合,由斜率相等求得a值.
解答 解:如图,
化目标函数z=ax+y(a>0)为y=-ax+z,
要使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,
则直线y=-ax+z与图中AC边所在直线重合,
即-a=$\frac{\frac{22}{5}-2}{1-5}=\frac{\frac{12}{5}}{-4}=-\frac{3}{5}$,∴a=$\frac{3}{5}$.
故选:B.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知直线mx+4y-2=0与2x-5y+1=0互相垂直,则m的值为( )
| A. | 10 | B. | 20 | C. | 0 | D. | -4 |
13.已知复数$z=\frac{1+i}{i}$,其中i为虚数单位,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
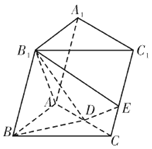 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.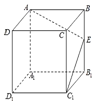 如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )
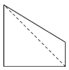
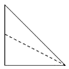
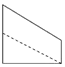
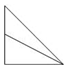
如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )