题目内容
(本小题满分14分)
已知椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 .圆
.圆 .
.
(1)求椭圆 的方程;
的方程;
(2)若直线
 与椭圆C有且只有一个公共点
与椭圆C有且只有一个公共点 ,且
,且 与圆
与圆 相交于
相交于 两点,
两点,
问
 是否成立?请说明理由.
是否成立?请说明理由.
(1) ;(2)
;(2)
 不成立.
不成立.
【解析】
试题分析:(1)由离心率为 ,可得:
,可得: ,由椭圆
,由椭圆 经过点
经过点 ,可得:
,可得: ,即可得椭圆
,即可得椭圆 的方程;(2)先将直线
的方程;(2)先将直线 的方程与椭圆
的方程与椭圆 的方程联立,可得
的方程联立,可得 ,利用
,利用 ,可得
,可得 ,再求出点
,再求出点 的坐标,进而可得点
的坐标,进而可得点 不是线段
不是线段 的中点,即可得
的中点,即可得
 不成立.
不成立.
试题解析:(1)【解析】
∵ 椭圆 过点
过点 ,
,
∴  . 1分
. 1分
∵ , 2分
, 2分
∴ . 3分
. 3分
∴椭圆 的方程为
的方程为 . 4分
. 4分
(2)解法1:由(1)知,圆 的方程为
的方程为 ,其圆心为原点
,其圆心为原点 . 5分
. 5分
∵直线 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点 ,
,
∴方程组 (*) 有且只有一组解.
(*) 有且只有一组解.
由(*)得 . 6分
. 6分
从而 ,化简得
,化简得 .① 7分
.① 7分
 ,
, . 9分
. 9分
∴ 点 的坐标为
的坐标为 . 10分
. 10分
由于 ,结合①式知
,结合①式知 ,
,
∴
 . 11分
. 11分
∴  与
与 不垂直. 12分
不垂直. 12分
∴ 点 不是线段
不是线段 的中点. 13分
的中点. 13分
∴
 不成立. 14分
不成立. 14分
解法2:由(1)知,圆 的方程为
的方程为 ,其圆心为原点
,其圆心为原点 . 5分
. 5分
∵直线 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点 ,
,
∴方程组 (*) 有且只有一组解.
(*) 有且只有一组解.
由(*)得 . 6分
. 6分
从而 ,化简得
,化简得 .① 7分
.① 7分
 , 8分
, 8分
由于 ,结合①式知
,结合①式知 ,
,
设 ,线段
,线段 的中点为
的中点为 ,
,
由 消去
消去 ,得
,得 . 9分
. 9分
∴  . 10分
. 10分
若 ,得
,得 ,化简得
,化简得 ,矛盾. 11分
,矛盾. 11分
∴ 点 与点
与点 不重合. 12分
不重合. 12分
∴ 点 不是线段
不是线段 的中点. 13分
的中点. 13分
∴ 
 不成立. 14分
不成立. 14分
考点:1、椭圆的方程;2、直线与圆锥曲线.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (
( )的焦点在圆
)的焦点在圆 外,则实数
外,则实数 的取值范围是 .
的取值范围是 . 的奇偶性相同,且在
的奇偶性相同,且在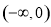 上单调性也相同的是
上单调性也相同的是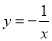 B.
B.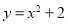
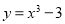 D.
D.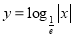
 的解集是 .
的解集是 . ,
, ,
, ,则实数
,则实数 的值是( )
的值是( ) B.
B.  C.
C.  D.
D. 
 与
与 的交点分别为
的交点分别为 ,
, ,则线段
,则线段 的垂直平分线的极坐标方程为 .
的垂直平分线的极坐标方程为 . 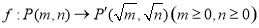 .设点
.设点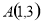 ,
,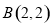 ,点
,点 是线段
是线段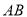 上一动点,
上一动点,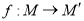 .当点
.当点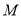 在线段
在线段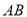 上从点
上从点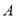 开始运动到点
开始运动到点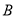 结束时,点
结束时,点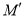 所经过的路线长度为( )
所经过的路线长度为( )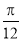 B.
B.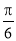 C.
C. 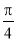 D.
D. 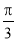
 =
= |
| |+b
|+b 0,方程
0,方程