题目内容
已知圆C的半径为2,圆心C在直线y=x-1上.
(Ⅰ)若圆心C也在直线x-2y=0上.
(ⅰ)求圆C的方程;
(ⅱ)若直线l:y=kx+1与圆C交于M,N两点,且
•
=2,求实数k的值.
(Ⅱ)已知A(0,3),若圆C上存在点P,使|PA|=2|PO|,求圆心C的横坐标a的取值范围.
(Ⅰ)若圆心C也在直线x-2y=0上.
(ⅰ)求圆C的方程;
(ⅱ)若直线l:y=kx+1与圆C交于M,N两点,且
| CM |
| CN |
(Ⅱ)已知A(0,3),若圆C上存在点P,使|PA|=2|PO|,求圆心C的横坐标a的取值范围.
考点:直线和圆的方程的应用
专题:
分析:(Ⅰ)(ⅰ)由
可得圆心C坐标,根据圆的半径,可得圆C的方程;
(ⅱ)利用
•
=2,求出∠MCN=60°,可得C到直线的距离为
,即可求实数k的值.
(Ⅱ)设P(x,y),由|PA|=2|PO|,利用两点间的距离公式列出关系式,整理后得到点P的轨迹为以(0,-1)为圆心,2为半径的圆,可记为圆D,由P在圆C上,得到圆C与圆D相交或相切,根据两圆的半径长,得出两圆心间的距离范围,利用两点间的距离公式列出不等式,求出不等式的解集,即可得到a的范围.
|
(ⅱ)利用
| CM |
| CN |
| 3 |
(Ⅱ)设P(x,y),由|PA|=2|PO|,利用两点间的距离公式列出关系式,整理后得到点P的轨迹为以(0,-1)为圆心,2为半径的圆,可记为圆D,由P在圆C上,得到圆C与圆D相交或相切,根据两圆的半径长,得出两圆心间的距离范围,利用两点间的距离公式列出不等式,求出不等式的解集,即可得到a的范围.
解答:
解:(Ⅰ)(ⅰ)由
可得
,即C(2,1),
∵圆C的半径为2,
∴圆C的方程为(x-2)2+(y-1)2=4;
(ⅱ)∵
•
=2,
∴2•2•cos∠MCN=2,
∴cos∠MCN=
,
∴∠MCN=60°,
∴C到直线的距离为
,
∴
=
,
∴k=±
;
(Ⅱ)设点P(x,y),由|PA|=2|PO|,知:
=2
,
化简得:x2+(y+1)2=4,
∴点P的轨迹为以(0,-1)为圆心,2为半径的圆,可记为圆D,
又∵点M在圆C上,
∴圆C与圆D的关系为相交或相切,
∴1≤|CD|≤3,其中|CD|=
,
∴1≤
≤3,
解得:0≤a≤
.
|
|
∵圆C的半径为2,
∴圆C的方程为(x-2)2+(y-1)2=4;
(ⅱ)∵
| CM |
| CN |
∴2•2•cos∠MCN=2,
∴cos∠MCN=
| 1 |
| 2 |
∴∠MCN=60°,
∴C到直线的距离为
| 3 |
∴
| |2k| | ||
|
| 3 |
∴k=±
| 3 |
(Ⅱ)设点P(x,y),由|PA|=2|PO|,知:
| x2+(y-3)2 |
| x2+y2 |
化简得:x2+(y+1)2=4,
∴点P的轨迹为以(0,-1)为圆心,2为半径的圆,可记为圆D,
又∵点M在圆C上,
∴圆C与圆D的关系为相交或相切,
∴1≤|CD|≤3,其中|CD|=
| a2+(2a-3)2 |
∴1≤
| a2+(2a-3)2 |
解得:0≤a≤
| 12 |
| 5 |
点评:此题考查点到直线的距离公式,以及圆与圆的位置关系的判定,涉及的知识有:两直线的交点坐标,直线的点斜式方程,两点间的距离公式,圆的标准方程,是一道综合性较强的试题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
已知在数列{an}中,a1=1,an+1-an=n(n∈N*),则a31的值为( )
| A、465 | B、466 |
| C、1275 | D、1276 |
执行如图所示的算法程序,则输出结果为( )


| A、2 | B、6 | C、42 | D、1806 |
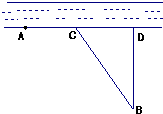 在甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在他们之间的此岸边合建一个污水处理厂C,从污水处理厂到甲厂和乙厂的铺设的排污管道费用分别为每千米3a元和5a元,记铺设管道的总费用为y元.
在甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在他们之间的此岸边合建一个污水处理厂C,从污水处理厂到甲厂和乙厂的铺设的排污管道费用分别为每千米3a元和5a元,记铺设管道的总费用为y元.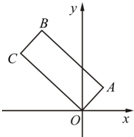 如图,矩形OABC的顶点O为原点,AB边所在直线的方程为3x+4y-25=0,顶点B的纵坐标为10.
如图,矩形OABC的顶点O为原点,AB边所在直线的方程为3x+4y-25=0,顶点B的纵坐标为10.