题目内容
如图,菱形ABCD中,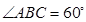 ,
,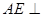 平面ABCD,
平面ABCD,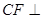 平面ABCD,
平面ABCD,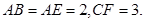
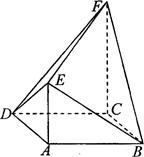
(1)求证: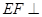 平面BDE;
平面BDE;
(2)求锐二面角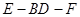 的大小.
的大小.
(1)证明:见解析;(2)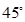 .
.
解析试题分析:(1)利用已有的垂直关系,以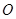 为原点,
为原点,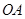 ,
, 为
为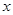 、
、 轴正向,
轴正向,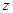 轴过
轴过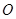 且平行于
且平行于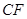 ,建立空间直角坐标系通过计算
,建立空间直角坐标系通过计算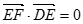 ,
,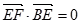 ,得到
,得到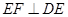 ,
,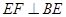 ,
,
达到证明目的.
(2)由知(1)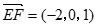 是平面
是平面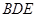 的一个法向量,
的一个法向量,
设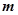
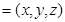 是平面
是平面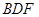 的一个法向量,利用
的一个法向量,利用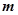
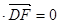 ,
, 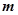
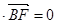
确定得到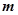
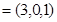 ,由
,由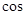 <
<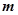 ,
,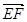 >
>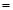 及二面角
及二面角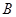 —
—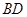 —
—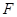 为锐二面角,得解.
为锐二面角,得解.
“向量法”往往能将复杂的证明问题,转化成计算问题,达到化繁为简,化难为易的目的.
试题解析:(1)证明:连接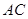 、
、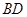 ,设
,设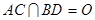 ,
,
∵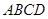 为菱形,∴
为菱形,∴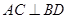 ,以
,以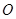 为原点,
为原点,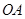 ,
, 为
为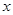 、
、 轴正向,
轴正向,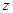 轴过
轴过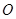 且平行于
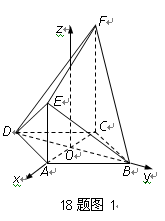
且平行于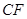 ,建立空间直角坐标系(图1), 2分
,建立空间直角坐标系(图1), 2分
则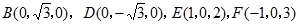 ,
,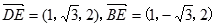 ,
,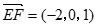 , 4分
, 4分
∴ 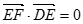 ,
,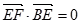 ,∴
,∴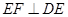 ,
,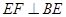 ,
,
又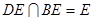 ,∴
,∴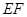 ⊥平面
⊥平面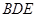 . 6分
. 6分
(2)由知(1)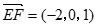 是平面
是平面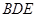 的一个法向量,
的一个法向量,
设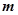
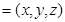 是平面
是平面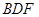 的一个法向量,
的一个法向量,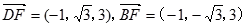 ,由
,由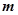
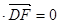 ,
, 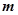
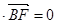

得: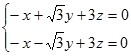 , 8分
, 8分
取 ,得
,得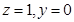 ,于是
,于是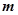
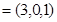
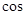 <
<

练习册系列答案
相关题目
 中,
中, 为正三角形,
为正三角形, 平面
平面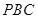 ,
, 为
为 的中点.
的中点.
 平面
平面 平面
平面 .
. 垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
 中,四边形
中,四边形 为菱形,
为菱形, ,四边形
,四边形 为矩形,若
为矩形,若 ,
, ,
, .
.
 面
面 ;
; 的余弦值;
的余弦值;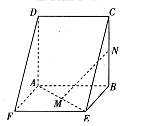
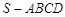 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面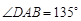 ,
, ,
,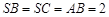 ,
,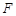 为线段
为线段 的中点.
的中点.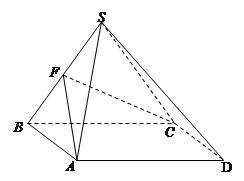
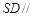 平面
平面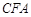 ;
;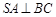 .
.
 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.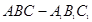 中,
中,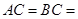
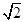 ,且
,且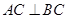 ,点
,点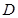 是
是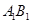 中点.
中点.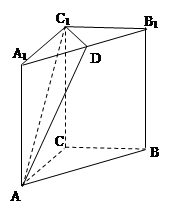
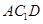 ⊥平面
⊥平面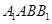 ;
;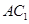 与平面
与平面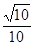 ,
,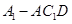 的体积.
的体积.