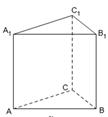
题目内容
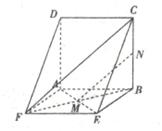
如图,边长为4的正方形ABCD与矩形ABEF所在平面互相垂直,M,N分别为AE,BC的中点,AF=3.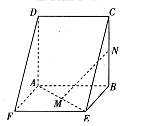
(I)求证:DA⊥平面ABEF;
(Ⅱ)求证:MN∥平面CDFE;
(Ⅲ)在线段FE上是否存在一点P,使得AP⊥MN? 若存在,求出FP的长;若不存在,请说明理由.
(I)详见解析;(Ⅱ)详见解析;(Ⅲ)存在,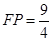
解析试题分析:(I)由面面垂直的性质定理可直接证得。(Ⅱ)将 转化为
转化为 的中点,利用中位线证
的中点,利用中位线证 ∥
∥ ,再根据线面平行的判定定理即可证MN∥平面CDFE。(Ⅲ)假设存在点P使AP⊥MN,由(I)易得
,再根据线面平行的判定定理即可证MN∥平面CDFE。(Ⅲ)假设存在点P使AP⊥MN,由(I)易得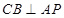 所以
所以 。(Ⅲ)由逆向思维可知只需证得
。(Ⅲ)由逆向思维可知只需证得 ,因为
,因为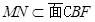 ,即可证得AP⊥MN。由相似三角形的相似比即可求得FP。
,即可证得AP⊥MN。由相似三角形的相似比即可求得FP。
试题解析:(I)因为 为正方形,所以
为正方形,所以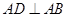 。
。
因为平面
 ,
,  ,
,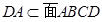 ,所以
,所以 .
.
(Ⅱ)连结
因为 是
是 的中点,且
的中点,且 为矩形,所以
为矩形,所以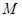 也是
也是 的中点。因为
的中点。因为 是
是 的中点,所以
的中点,所以 ∥
∥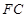 ,因为
,因为 ,所以MN∥平面CDFE。
,所以MN∥平面CDFE。
(Ⅲ)过点 作
作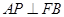 交线段
交线段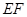 于点
于点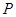 ,则点
,则点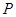 即为所求。因为ABCD为正方形,所以
即为所求。因为ABCD为正方形,所以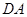 ∥
∥ 。因为
。因为 ,所以
,所以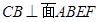 ,因为
,因为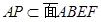 ,所以
,所以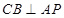 。因为
。因为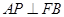 ,且
,且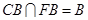 ,所以
,所以 ,因为
,因为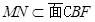 ,所以
,所以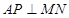 。因为
。因为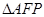 与
与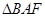 相似,所以
相似,所以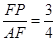 ,因为
,因为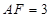 ,所以
,所以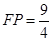 。
。
考点:线线平行、线面平行、线线垂直、线面垂直。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为直角梯形,
为直角梯形, ,
, 平面
平面
 平面
平面 ;
; 所成锐二面角的余弦值.
所成锐二面角的余弦值. 中,E为
中,E为 的中点.
的中点.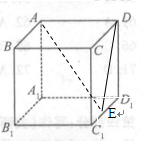
 ;
;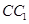 所成的角的正弦值.
所成的角的正弦值.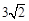 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且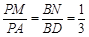 .
.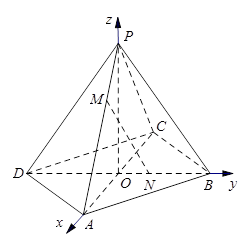
 中,点
中,点 分别是棱
分别是棱 的中点.
的中点.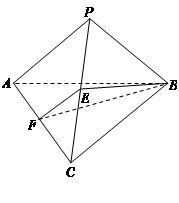
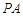 //平面
//平面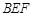 ;
;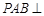 平面
平面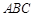 ,
,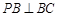 ,求证:
,求证: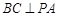 .
.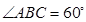 ,
,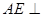 平面ABCD,
平面ABCD,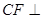 平面ABCD,
平面ABCD,
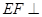 平面BDE;
平面BDE;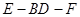 的大小.
的大小. 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且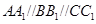 ,
,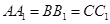 .
.
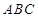 //平面
//平面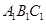 ;
;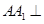 平面
平面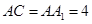 ,
,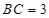 ,
,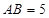 ,求证:
,求证: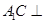 平面
平面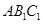 ;
;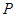 为
为 上的动点,求当
上的动点,求当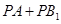 取得最小值时
取得最小值时 的长.
的长.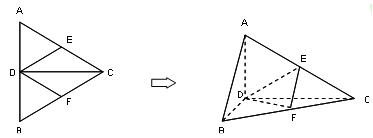
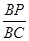 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. 为正方形,平面
为正方形,平面 为等腰梯形,
为等腰梯形, ,
,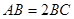 ,
, ,
, .
.
 平面
平面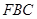 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.