题目内容
在四棱锥 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 中点,又
中点,又 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
(1)求证: ;
;
(2)求证: 平面
平面 ;
;
(3)求二面角 的余弦值.
的余弦值.
(1)详见解析;(2)详见解析;(3)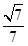
解析试题分析:(1)线线垂直是通过线面垂直证明,由已知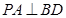 ,
,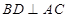 ,从而
,从而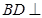 平面
平面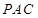 ,进而可证明
,进而可证明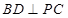 ;(2)要证明直线和平面平行,只需在平面内找一条直线与之平行即可,该题中通过计算得
;(2)要证明直线和平面平行,只需在平面内找一条直线与之平行即可,该题中通过计算得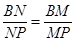 ,从而说明
,从而说明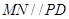 ,进而证明
,进而证明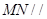 面
面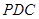 ;(3)二面角的求法:根据已知条件选三条两两垂直的直线,分别作为
;(3)二面角的求法:根据已知条件选三条两两垂直的直线,分别作为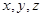 轴,建立空间直角坐标系,表示相关点的坐标,并求二面角两个半平面的法向量,再求法向量的夹角,通过观察二面角是锐二面角还是钝二面角,决定二面角余弦值的正负,该题中,可选
轴,建立空间直角坐标系,表示相关点的坐标,并求二面角两个半平面的法向量,再求法向量的夹角,通过观察二面角是锐二面角还是钝二面角,决定二面角余弦值的正负,该题中,可选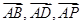 的方向为
的方向为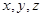 轴的正方向,而且面
轴的正方向,而且面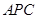 的法向量就是
的法向量就是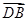 ,故只需求面
,故只需求面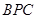 的法向量即可.
的法向量即可.
试题解析:(I) 因为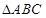 是正三角形,
是正三角形,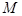 是
是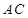 中点,所以
中点,所以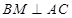 ,即
,即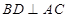 ,又因为
,又因为 ,
,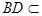 平面
平面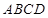 ,
,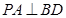 ,又
,又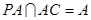 ,所以
,所以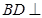 平面
平面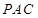 ,
,
又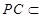 平面
平面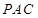 ,所以
,所以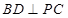 .
.
(Ⅱ)在正三角形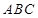 中,
中,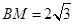 , 在
, 在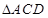 中,因为
中,因为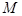 为
为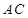 中点,
中点,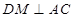 ,所以
,所以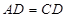
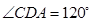 ,所以
,所以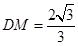 ,所以
,所以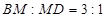 ,在等腰直角三角形
,在等腰直角三角形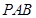 中,
中,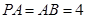 ,
,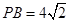 ,所以
,所以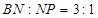 ,
,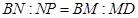 ,所以
,所以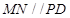 ,又
,又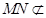 平面
平面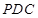 ,
,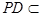 平面
平面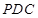 ,所以
,所以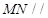 平面
平面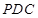 .
.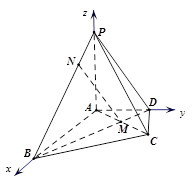
(Ⅲ)因为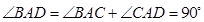 ,所以
,所以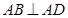 ,分别以
,分别以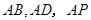 为
为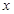 轴,
轴, 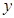 轴,
轴, 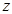 轴建立如图的空间直角坐标系,所以
轴建立如图的空间直角坐标系,所以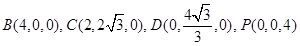
由(Ⅱ)可知,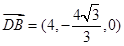 为平面
为平面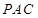 的法向量 ,
的法向量 ,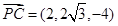 ,
,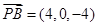
设平面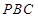 的一个法向量为
的一个法向量为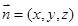 ,则
,则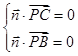 ,即
,即 ,令
,令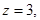 则平面
则平面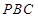 的一个法向量为
的一个法向量为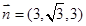 , 设二面角
, 设二面角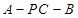 的大小为
的大小为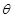 , 则
, 则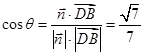

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正方体 的棱长为
的棱长为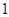 ,线段
,线段 上有两个动点
上有两个动点 ,且
,且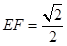 ,则下列结论中错误的是( )
,则下列结论中错误的是( )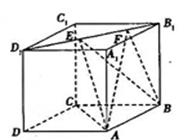
A.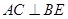 |
B.三棱锥 的体积为定值 的体积为定值 |
C.二面角 的大小为定值 的大小为定值 |
D.异面直线 所成角为定值 所成角为定值 |
 ACD沿AC折起至
ACD沿AC折起至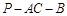 为600,G,H分别是PA,PC的中点.
为600,G,H分别是PA,PC的中点.
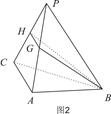
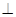 平面BGH;
平面BGH;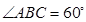 ,
,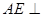 平面ABCD,
平面ABCD,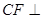 平面ABCD,
平面ABCD,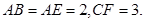
 平面BDE;
平面BDE;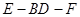 的大小.
的大小. 中,底面
中,底面 为菱形,
为菱形, 平面
平面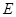 为
为 的中点,
的中点,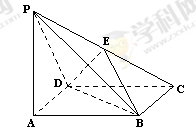
 平面
平面 ; (II)平面
; (II)平面 ⊥平面
⊥平面 .
.
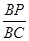 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.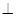 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF,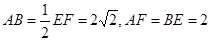 ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.
 (侧棱和底面垂直的棱柱)中,平面
(侧棱和底面垂直的棱柱)中,平面 侧面
侧面 ,
,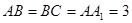 ,
, ,且满足
,且满足 .
.
 ;
;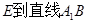 的距离;
的距离; 的平面角的余弦值.
的平面角的余弦值. 平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.