题目内容
13.复数z满足z(4+i)=3+i,则复数z在复平面内对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 把已知等式变形,利用复数代数形式的乘除运算化简,求出z的坐标得答案.
解答 解:由z(4+i)=3+i,得
$z=\frac{3+i}{4+i}=\frac{(3+i)(4-i)}{(4+i)(4-i)}=\frac{13+i}{17}=\frac{13}{17}+\frac{1}{17}i$,
∴复数z在复平面内对应的点的坐标为($\frac{13}{17},\frac{1}{17}$),位于第一象限.
故选:A.
点评 本题考查复数的代数表示法及其几何意义,是基础题的计算题.

练习册系列答案
相关题目
18.对于实数a>0,“$\frac{1}{x}$<a”是“x>$\frac{1}{a}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.已知圆O:x2+y2=1,点P为直线x-2y-3=0上一动点,过点P向圆O引两条切线PA,PB,A、B为切点,则直线AB经过定点( )
| A. | (2,0) | B. | (3,0) | C. | ($\frac{1}{2}$,-1) | D. | ($\frac{1}{3}$,-$\frac{2}{3}$) |
5.已知k∈R,点P(a,b)是直线x+y=2k与圆x2+y2=k2-2k+3的公共点,则ab的最大值为( )
| A. | 15 | B. | 9 | C. | 1 | D. | -$\frac{5}{3}$ |
3.如表示意某科技公司2012~2016年年利润y(单位:十万元)与年份代号x之间的关系,如果该公司盈利变化规律保持不变,则第n年(以2012年为第1年)年利润的预报值是y=2n2-n.(直接写出代数式即可,不必附加单位)
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 |
| 年利润/十万元 | 1 | 6 | 15 | 28 | 45 |
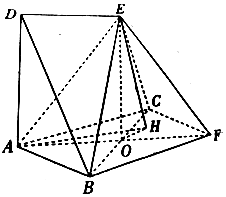 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°