题目内容
设 是一个三次函数,
是一个三次函数,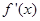 为其导函数.如图所示是函数
为其导函数.如图所示是函数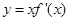 的图像的一部分,则
的图像的一部分,则 的极大值与极小值分别为( )
的极大值与极小值分别为( )
 是一个三次函数,
是一个三次函数,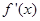 为其导函数.如图所示是函数
为其导函数.如图所示是函数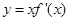 的图像的一部分,则
的图像的一部分,则 的极大值与极小值分别为( )
的极大值与极小值分别为( )
A. 与 与 | B. 与 与 |
C. 与 与 | D. 与 与 |
C
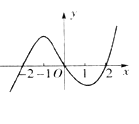
本题考查导数的应用。如图所示:由函数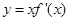 的图像知,
的图像知,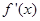 有两个零点-2、2当x<-2时,
有两个零点-2、2当x<-2时, >0,当0>x>-2时,
>0,当0>x>-2时, <0,故
<0,故 的极大值为
的极大值为 ,同理得
,同理得 的极小值为
的极小值为 。
。
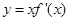 的图像知,
的图像知,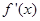 有两个零点-2、2当x<-2时,
有两个零点-2、2当x<-2时, >0,当0>x>-2时,
>0,当0>x>-2时, <0,故
<0,故 的极大值为
的极大值为 ,同理得
,同理得 的极小值为
的极小值为 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
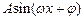 (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧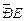 .
.
 ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时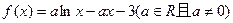 .
.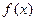 的单调区间;
的单调区间;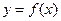 的图像在点
的图像在点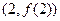 处的切线的倾斜角为
处的切线的倾斜角为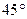 ,问:
,问: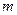 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的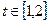 ,函数
,函数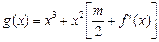 在区间
在区间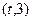 上总存在极值?
上总存在极值?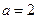 时,设函数
时,设函数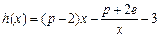 ,若在区间
,若在区间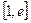 上至少存在
上至少存在 一个
一个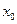 ,
,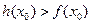 成立,试求实数
成立,试求实数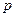 的取值范围.
的取值范围. 2分)若存在实数
2分)若存在实数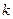 和
和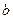 ,使得函数
,使得函数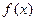 与
与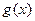 对其定义域上的任意实数
对其定义域上的任意实数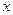 分别满足
分别满足 :
: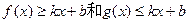 ,则称直线
,则称直线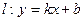 为
为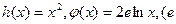 为自然对数的底数);
为自然对数的底数);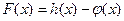 的极值;
的极值;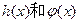 是否存在和谐直线?若存在,求出此和谐直线方程;若不存在,请说明理由.
是否存在和谐直线?若存在,求出此和谐直线方程;若不存在,请说明理由.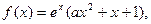
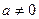 时,求:函数
时,求:函数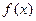 的单调区间;
的单调区间;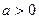 时,求证:当
时,求证:当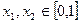 时,不等式
时,不等式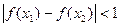
 .
.
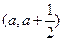 其中a >0,上存在极
其中a >0,上存在极 值,求实数a的取值范
值,求实数a的取值范 围;
围; 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;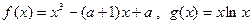
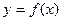 ,
,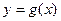 在
在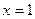 处的切线相互垂直,求这两个切线方程.
处的切线相互垂直,求这两个切线方程.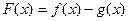 单调递增,求
单调递增,求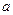 的范围.
的范围. 的导函数为
的导函数为 ,则
,则 (
( 为虚数单位)的值为( )
为虚数单位)的值为( ) 的一个极值点.(Ⅰ)求
的一个极值点.(Ⅰ)求 ;(Ⅱ)求函数
;(Ⅱ)求函数 的单调区间;(Ⅲ)若直线
的单调区间;(Ⅲ)若直线 与函数
与函数 的图像有
的图像有 个交点,求
个交点,求 的取值范围.
的取值范围.